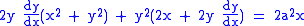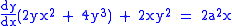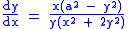Kappa curve
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the kappa curve or Gutschoven's curve is a two-dimensional algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
resembling the Greek letter
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
κ (kappa).
Using the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
it can be expressed as:
or, using parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
s:
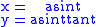
In polar coordinates its equation is even simpler:
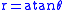
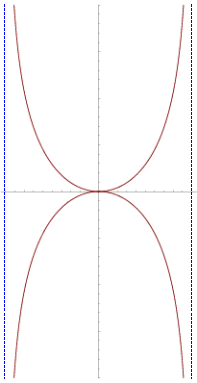
It has two vertical asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s at
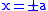, shown as dashed blue lines in the figure at right.The kappa curve's curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
:
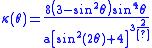
Tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
ial angle:
The kappa curve was first studied by Gérard van Gutschoven around 1662. Other famous mathematicians who have studied it include Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Johann Bernoulli
Johann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
.
Its tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
s were first calculated by Isaac Barrow
Isaac Barrow
Isaac Barrow was an English Christian theologian, and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for the discovery of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was...
in the 17th century.
Derivative
By using implicit differentiation, it is possible to find that the derivative of the kappa curve is:
