
Kaup–Kupershmidt equation
Encyclopedia
The Kaup–Kupershmidt equation (named after David J. Kaup and Boris Abram Kupershmidt) is the nonlinear fifth-order partial differential equation
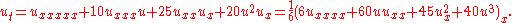
In addition to it being the first equation in a hierarchy of integrable equations
with Lax operator
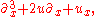
it is also the second non-trivial equation in the KdV hierarchy
- the first of which is the KdV equation.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
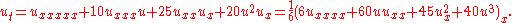
In addition to it being the first equation in a hierarchy of integrable equations
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
with Lax operator
Lax pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
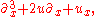
it is also the second non-trivial equation in the KdV hierarchy
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
- the first of which is the KdV equation.

