
Kerr-Newman metric
Encyclopedia
The Kerr–Newman metric is a solution of the Einstein–Maxwell equations in general relativity
, describing the spacetime geometry in the region surrounding a charged, rotating mass. It is assumed that the cosmological constant
equals zero. This solution has not been especially useful for describing astrophysical phenomena, because observed astronomical objects do not possess an appreciable net electric charge
, and the cosmological constant
is now thought to be non-zero. The solution has instead been of primarily theoretical and mathematical interest.
found the axisymmetric solution of Einstein's field equation for a black hole which is both rotating and electrically charged. This formula for the metric tensor
 is called the Kerr–Newman metric. It is a generalisation of the Kerr metric
is called the Kerr–Newman metric. It is a generalisation of the Kerr metric
for an uncharged spinning point-mass, which had been discovered by Roy Kerr
two years earlier.
Four related solutions may be summarized by the following table:
where Q represents the body's electric charge
and J represents its spin angular momentum
.
in the vicinity of a rotating mass M with charge Q. The formula for this metric depends upon what coordinates or coordinate conditions
are selected. One way to express this metric is by writing down its line element
in a particular set of spherical coordinates
:
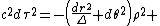
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, describing the spacetime geometry in the region surrounding a charged, rotating mass. It is assumed that the cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
equals zero. This solution has not been especially useful for describing astrophysical phenomena, because observed astronomical objects do not possess an appreciable net electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, and the cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
is now thought to be non-zero. The solution has instead been of primarily theoretical and mathematical interest.
History
In 1965, Ezra "Ted" NewmanEzra T. Newman
Ezra Ted Newman is an American physicist, known for his many contributions to general relativity theory. He is Professor Emeritus at the University of Pittsburgh...
found the axisymmetric solution of Einstein's field equation for a black hole which is both rotating and electrically charged. This formula for the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
 is called the Kerr–Newman metric. It is a generalisation of the Kerr metric
is called the Kerr–Newman metric. It is a generalisation of the Kerr metricKerr metric
The Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
for an uncharged spinning point-mass, which had been discovered by Roy Kerr
Roy Kerr
Roy Patrick Kerr CNZM is a New Zealand mathematician who is best known for discovering the Kerr vacuum, an exact solution to the Einstein field equation of general relativity...
two years earlier.
Four related solutions may be summarized by the following table:
| Non-rotating (J = 0) | Rotating (J ≠ 0) | |
| Uncharged (Q = 0) | Schwarzschild Schwarzschild metric In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or... |
Kerr Kerr metric The Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which... |
| Charged (Q ≠ 0) | Reissner–Nordström | Kerr–Newman |
where Q represents the body's electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and J represents its spin angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
.
Mathematical form
The Kerr–Newman metric describes the geometry of spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
in the vicinity of a rotating mass M with charge Q. The formula for this metric depends upon what coordinates or coordinate conditions
Coordinate conditions
In general relativity, the laws of physics can be expressed in a generally covariant form. In other words, the real world does not care about our coordinate systems. However, it is often useful to fix upon a particular coordinate system, in order to solve actual problems or make actual predictions...
are selected. One way to express this metric is by writing down its line element
Line element
A line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
in a particular set of spherical coordinates
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
:
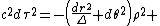
-
-
-

where the coordinates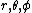 are standard spherical coordinate systemSpherical coordinate systemIn mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
are standard spherical coordinate systemSpherical coordinate systemIn mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
.- rs is the Schwarzschild radiusSchwarzschild radiusThe Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
(in meters) of the massive body, which is related to its mass M by
-

- where G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, and - rQ is a length-scale corresponding to the electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
Q of the mass
-
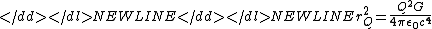
- where 1/4πε0 is Coulomb's force constantCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
.
The length-scales α, ρ and Δ have been introduced for brevity.
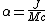

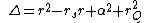
Alternative (Kerr–Schild) formulation
The Kerr–Newman metric can be expressed in "Kerr–Schild" form, using a particular set of Cartesian coordinatesCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
as follows. These solutions were proposed by Kerr and SchildSchildSchild is the surname of:* Alfred Schild , a leading American physicist , Austrian female alpine skier* Charles Schild , an American inventor...
in 1965.
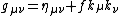


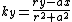

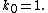
Notice that is a unit vector. Here "M" is the constant mass of the spinning object, "Q" is the constant charge of the spinning object, "
is a unit vector. Here "M" is the constant mass of the spinning object, "Q" is the constant charge of the spinning object, "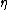 " is the Minkowski tensor, and "
" is the Minkowski tensor, and " " is a constant rotational parameter of the spinning object. It is understood that the vector
" is a constant rotational parameter of the spinning object. It is understood that the vector 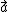 is directed along the positive z-axis. The quantity "r" is not the radius, but rather is implicitly defined like this:
is directed along the positive z-axis. The quantity "r" is not the radius, but rather is implicitly defined like this:
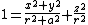 .
.
Notice that the quantity "r" becomes the usual radius when the rotational parameter "a" approaches zero. In this form of solution, units are selected so that the speed of light is unity (c=1). In order to provide a complete solution of the Einstein–Maxwell Equations, the Kerr–Newman solution not only includes a formula for the metric tensor, but also a formula for the electromagnetic potential:
when the rotational parameter "a" approaches zero. In this form of solution, units are selected so that the speed of light is unity (c=1). In order to provide a complete solution of the Einstein–Maxwell Equations, the Kerr–Newman solution not only includes a formula for the metric tensor, but also a formula for the electromagnetic potential:

At large distances from the source (R>>a), these equations reduce to the Reissner-Nordstrom metricReissner-Nordström metricIn physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein-Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M.-The metric:...
with:

In the Kerr–Schild form of the Kerr–Newman metric, the determinant of the metric tensor is everywhere equal to negative one, even near the source.
Special cases and generalizations
The Kerr–Newman metric is a generalization of other exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
:- Kerr metricKerr metricThe Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
if the charge Q is zero. - Reissner–Nordström metric if the angular momentum J (or a) is zero.
- Schwarzschild metricSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
if the charge Q and the angular momentum J (or a) are zero. - Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
if the gravitational constant G is zero (with electric and magnetic fields more complicated than simply the fields of a charged magnetic dipole).
The Kerr–Newman solution (with cosmological constant equal to zero) is also a special case of more general exact solutions of the Einstein–Maxwell Equations.
Some aspects of the solution
Newman's result represents the simplest stationaryStationary spacetimeIn general relativity, specifically in the Einstein field equations, a spacetime is said to be stationary if it admits a Killing vector that is asymptotically timelike....
, axisymmetricAxial symmetryAxial symmetry is symmetry around an axis; an object is axially symmetric if its appearance is unchanged if rotated around an axis . For example, a baseball bat or a tea saucer looks the same if it is rotated by any angle about the line passing lengthwise through its center, so it is axially...
, asymptotically flat solution of Einstein's equations in the presence of an electromagnetic fieldElectromagnetic fieldAn electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
in four dimensions. It is sometimes referred to as an "electrovacuum" solution of Einstein's equations.
Any Kerr–Newman source has its rotation axis aligned with its magnetic axis. Thus, a Kerr–Newman source is different from commonly observed astronomical bodies, for which there is a substantial angle between the rotation axis and the magnetic momentMagnetic momentThe magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
.
If the Kerr–Newman potential is considered as a model for a classical electron, it predicts an electron having not just a magnetic dipole moment, but also other multipole moments, such as an electric qrupole moment. As of yet, an electron qrupole moment has not been detected empirically.
In the G=0 limit, the electromagnetic fields are those of a charged rotating disk inside a ring where the fields are infinite. The total field energy for this disk is infinite, and so this G=0 limit does not solve the problem of infinite self-energySelf-energyIn theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
.
Like the Kerr metricKerr metricThe Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
for an uncharged rotating mass, the Kerr–Newman interior solution exists mathematically but is probably not representative of the actual metric of a physically realistic rotating black holeRotating black holeA rotating black hole is a black hole that possesses spin angular momentum.-Types of black holes:There are four known, exact, black hole solutions to Einstein's equations, which describe gravity in General Relativity. Two of these rotate...
due to stability issues. Although it represents a generalization of the Kerr metric, it is not considered as very important for astrophysical purposes since one does not expect that realistic black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s have an important electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
.
The Kerr–Newman metric defines a black hole with an event horizon only when the following relation is satisfied:
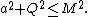
An electron's a and Q (suitably specified in geometrized units) both exceed its mass M, in which case the metric has no event horizon and thus there can be no such thing as a black hole electronBlack hole electronIn physics, there is a speculative notion that if there were a black hole with the same mass and charge as an electron, it would share many of the properties of the electron including the magnetic moment and Compton wavelength. This idea is substantiated within a series of papers published by...
— only a nakedNaked singularityIn general relativity, a naked singularity is a gravitational singularity, without an event horizon. In a black hole, there is a region around the singularity, the event horizon, where the gravitational force of the singularity is strong enough so that light cannot escape. Hence, the singularity...
spinning ring singularity. Such a metric has several seemingly unphysical properties, such as the ring's violation of the cosmic censorship hypothesisCosmic censorship hypothesisThe weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of singularities arising in general relativity....
, and also appearance of causality-violating closed timelike curveClosed timelike curveIn mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
s in the immediate vicinity of the ring.
The Russian theorist Alexander Burinskii wrote in 2007: "In this work we obtain an exact correspondence between the wave function of the Dirac equation and the spinor (twistorial) structure of the Kerr geometry. It allows us to assume that the Kerr–Newman geometry reflects the specific space-time structure of electron, and electron contains really the Kerr-Newman circular string of Compton size". The Burinskii paper describes an electron as a gravitationally confined ring singularity without an event horizon. It has some, but not all of the predicted properties of a black hole.
The electromagnetic fields
The electric and magnetic fields can be obtained in the usual way by differentiating the four-potential to obtain the electromagnetic field strength tensorElectromagnetic tensorThe electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
. It will be convenient to switch over to three-dimensional vector notation.
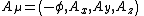
The static electric and magnetic fields are derived from the vector potential and the scalar potential like this:
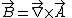
Using the Kerr-Newman formula for the four-potential in the Kerr-Schild form yields the following concise complex formula for the fields:
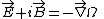
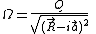
The quantity omega (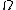 ) in this last equation is similar to the Coulomb potential, except that the radius vector is shifted by an imaginary amount. This complex potential was discussed as early as the nineteenth century, by the French mathematician Paul Émile AppellPaul Émile AppellPaul Appell , also known as Paul Émile Appel, was a French mathematician and Rector of the University of Paris...
) in this last equation is similar to the Coulomb potential, except that the radius vector is shifted by an imaginary amount. This complex potential was discussed as early as the nineteenth century, by the French mathematician Paul Émile AppellPaul Émile AppellPaul Appell , also known as Paul Émile Appel, was a French mathematician and Rector of the University of Paris...
.
External links
- where 1/4πε0 is Coulomb's force constant
- where G is the gravitational constant
- rs is the Schwarzschild radius
-
-

