Kinetic Monte Carlo
Encyclopedia
The kinetic Monte Carlo method is a Monte Carlo method
computer simulation intended to simulate the time evolution of some processes occurring in nature. Typically these are processes that occur with a given known rate. It is important to understand that these rates are inputs to the KMC algorithm, the method itself cannot predict them.
The KMC method is essentially the same as the dynamic Monte Carlo method
and the Gillespie algorithm
, the main difference seems to be in terminology and usage areas: KMC is used mainly in physics while the "dynamic" method is mostly used in chemistry.
(Note: because the average value of
is equal to unity, the same average time scale can be obtained by instead using 
in step 8. In this case, however, the delay associated with transition i will not be drawn from the Poisson distribution
described by
, but will instead be the mean of that distribution.)
This algorithm is known in different sources variously as the residence-time algorithm or the n-fold way or the Bortz-Kalos-Lebowitz (BKL) algorithm or just the kinetic Monte Carlo (KMC) algorithm. It is important to note that the timestep involved is a function of the probability that all events i, did not occur.
are time dependent, step 7 has to be modified by (Prados 1997):
.
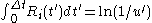The reaction (step 5) has to be chosen after this by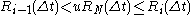
Another very similar algorithm is called the First Reaction Method (FRM). It consists of choosing the first-occurring reaction, meaning to choose the smallest time
, and the corresponding reaction number i, from the formula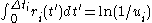
,
where the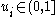
are N random numbers.
type, and if different processes are independent (i.e. not correlated) then the KMC algorithm gives the correct time scale for the evolution of the simulated system.
If furthermore the transitions follow detailed balance
, the KMC algorithm can be used to simulate thermodynamic equilibrium. However, KMC is widely used to simulate non-equilibrium processes (Meng 1994), in which case detailed balance need not be obeyed.
The KMC algorithm is efficient in the sense that every iteration is guaranteed to produce a transition. However, in the form presented above it requires
operations for each transition, which is not too efficient. In many cases this can be much improved on by binning the same kinds of transitions into bins, and/or forming a tree data structure of the events. A constant-time scaling algorithm of this type has recently been developed and tested in (Slepoy 2008).
The major disadvantage with KMC is that all possible rates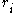
and reactions have to be known in advance. The method itself can do nothing about predicting them.
To give an idea what the "objects" and "events" may be in practice, here is one concrete simple example, corresponding to example 2 above.
Consider a system where individual atoms are deposited on a surface one at a time (typical of physical vapor deposition
), but also may migrate on the surface with some known jump rate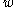
. In this case the "objects" of the KMC algorithm are simply the individual atoms.
If two atoms come right next to each other, they become immobile. Then the flux of incoming atoms determines a rate rdeposit, and the system can be simulated with KMC considering all deposited mobile atoms which have not (yet) met a counterpart and become immobile. This way there are the following events possible at each KMC step:
An already deposited atom jumps one step with rate w.
After an event has been selected and carried out with the KMC algorithm, one then needs to check whether the new or just jumped atom has become immediately adjacent to some other atom. If this has happened, the atom(s) which are now adjacent needs to be moved away from the list of mobile atoms, and correspondingly their jump events removed from the list of possible events.
Naturally in applying KMC to problems in physics and chemistry, one has to first consider whether the real system follows the assumptions underlying KMC well enough.
Real processes do not necessarily have well-defined rates, the
transition processes may be correlated, in case of atom or particle jumps
the jumps may not occur in random directions, and so on. When simulating
widely disparate time scales one also needs to consider whether
new processes may be present at longer time scales. If any of these
issues are valid, the time scale and system evolution predicted by KMC
may be skewed or even completely wrong.
Apparently independent of the work of Young and Elcock, Bortz, Kalos and Lebowitz (Bortz 1975) developed a KMC algorithm for simulating the Ising model
, which they called the n-fold way. The basics of their algorithm is the same as that of (Young 1966), but they do provide much greater detail on the method.
The following year Dan Gillespie published what is now known as the Gillespie algorithm
to describe chemical reactions (Gillespie 1976). The algorithm is similar and the time advancement scheme essentially the same as in KMC.
There is as of the writing of this (June 2006) no definitive treatise of the theory of KMC, but Fichthorn and Weinberg have discussed the theory for thermodynamic equilibrium KMC simulations in detail in (Fichthorn 1991). A good introduction is given also by Art Voter (Voter 2005),http://www.ipam.ucla.edu/publications/matut/matut_5898_preprint.pdf and by A.P.J. Jansen (Jansen 2003),http://arxiv.org/abs/cond-mat/0303028,
and a recent review is (Chatterjee 2007) or (Chotia 2008).
In March, 2006 the, probably, first commercial software using Kinetic Monte Carlo to simulate the diffusion and activation/deactivation of dopants in Silicon and Silicon-like materials is released by Synopsys
, reported by Martin-Bragado et al. (Martin-Bragado 06).
occurring. At least the following subdivisions are used:
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
computer simulation intended to simulate the time evolution of some processes occurring in nature. Typically these are processes that occur with a given known rate. It is important to understand that these rates are inputs to the KMC algorithm, the method itself cannot predict them.
The KMC method is essentially the same as the dynamic Monte Carlo method
Dynamic Monte Carlo method
In chemistry, dynamic Monte Carlo is a method for modeling the dynamic behaviors of molecules by comparing the rates of individual steps with random numbers...
and the Gillespie algorithm
Gillespie algorithm
In probability theory, the Gillespie algorithm generates a statistically correct trajectory of a stochastic equation. It was created by Joseph L...
, the main difference seems to be in terminology and usage areas: KMC is used mainly in physics while the "dynamic" method is mostly used in chemistry.
Algorithm
The KMC algorithm for simulating the time evolution of a system where some processes can occur with known rates r can be written for instance as follows: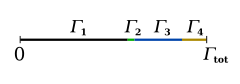- Set the time
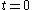. - Form a list of all possible rates in the system
- Calculate the cumulative function
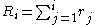for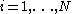 
, where N is the total number of transitions. - Get a uniform random number
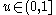
- Find the event to carry out i by finding the i for which
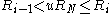(this can be achieved efficiently using binary search). - Carry out event i.
- Get a new uniform random number
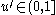. - Update the time with
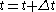, where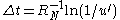 
- Recalculate all rates
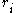which may have changed due to the transition. If appropriate, remove or add new transitions i. Update N and the list of events accordingly. - Return to step 2.
(Note: because the average value of
is equal to unity, the same average time scale can be obtained by instead using 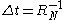in step 8. In this case, however, the delay associated with transition i will not be drawn from the Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
described by
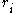, but will instead be the mean of that distribution.)This algorithm is known in different sources variously as the residence-time algorithm or the n-fold way or the Bortz-Kalos-Lebowitz (BKL) algorithm or just the kinetic Monte Carlo (KMC) algorithm. It is important to note that the timestep involved is a function of the probability that all events i, did not occur.
Time-dependent Algorithms
If the rates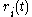 are time dependent, step 7 has to be modified by (Prados 1997):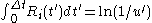.The reaction (step 5) has to be chosen after this by
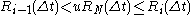
Another very similar algorithm is called the First Reaction Method (FRM). It consists of choosing the first-occurring reaction, meaning to choose the smallest time
, and the corresponding reaction number i, from the formula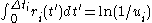,where the
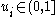are N random numbers.Comments on the algorithm
The key property of the KMC algorithm (and of the FRM one) is that if the rates are correct, if the processes associated with the rates are of the Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
type, and if different processes are independent (i.e. not correlated) then the KMC algorithm gives the correct time scale for the evolution of the simulated system.
If furthermore the transitions follow detailed balance
Detailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
, the KMC algorithm can be used to simulate thermodynamic equilibrium. However, KMC is widely used to simulate non-equilibrium processes (Meng 1994), in which case detailed balance need not be obeyed.
The KMC algorithm is efficient in the sense that every iteration is guaranteed to produce a transition. However, in the form presented above it requires
operations for each transition, which is not too efficient. In many cases this can be much improved on by binning the same kinds of transitions into bins, and/or forming a tree data structure of the events. A constant-time scaling algorithm of this type has recently been developed and tested in (Slepoy 2008).The major disadvantage with KMC is that all possible rates
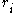and reactions have to be known in advance. The method itself can do nothing about predicting them.Examples of use
KMC has been used in simulations of the e.g. the following physical systems:- Surface diffusion
- Surface growth (Meng 1996)
- Vacancy diffusion in alloys (this was the original use in (Young 1966))
- Coarsening of domain evolution
- Defect mobility and clustering in ion or neutron irradiated solids including, but not limited to, damage accumulation and amorphization/recrystallization models.
- Viscoelasticity of physically crosslinked networks (Baeurle 2006)
To give an idea what the "objects" and "events" may be in practice, here is one concrete simple example, corresponding to example 2 above.
Consider a system where individual atoms are deposited on a surface one at a time (typical of physical vapor deposition
Physical vapor deposition
Physical vapor deposition is a variety of vacuum deposition and is a general term used to describe any of a variety of methods to deposit thin films by the condensation of a vaporized form of the desired film material onto various workpiece surfaces...
), but also may migrate on the surface with some known jump rate
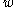. In this case the "objects" of the KMC algorithm are simply the individual atoms.If two atoms come right next to each other, they become immobile. Then the flux of incoming atoms determines a rate rdeposit, and the system can be simulated with KMC considering all deposited mobile atoms which have not (yet) met a counterpart and become immobile. This way there are the following events possible at each KMC step:
- A new atom comes in with rate 'r
After an event has been selected and carried out with the KMC algorithm, one then needs to check whether the new or just jumped atom has become immediately adjacent to some other atom. If this has happened, the atom(s) which are now adjacent needs to be moved away from the list of mobile atoms, and correspondingly their jump events removed from the list of possible events.
Naturally in applying KMC to problems in physics and chemistry, one has to first consider whether the real system follows the assumptions underlying KMC well enough.
Real processes do not necessarily have well-defined rates, the
transition processes may be correlated, in case of atom or particle jumps
the jumps may not occur in random directions, and so on. When simulating
widely disparate time scales one also needs to consider whether
new processes may be present at longer time scales. If any of these
issues are valid, the time scale and system evolution predicted by KMC
may be skewed or even completely wrong.
History
The first publication which described the basic features of the KMC method (namely using a cumulative function to select an event and a time scale calculation of the form 1/R) was by Young and Elcock in 1966 (Young 1966). The residence-time algorithm was also published at about the same time in (Cox 1965).Apparently independent of the work of Young and Elcock, Bortz, Kalos and Lebowitz (Bortz 1975) developed a KMC algorithm for simulating the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, which they called the n-fold way. The basics of their algorithm is the same as that of (Young 1966), but they do provide much greater detail on the method.
The following year Dan Gillespie published what is now known as the Gillespie algorithm
Gillespie algorithm
In probability theory, the Gillespie algorithm generates a statistically correct trajectory of a stochastic equation. It was created by Joseph L...
to describe chemical reactions (Gillespie 1976). The algorithm is similar and the time advancement scheme essentially the same as in KMC.
There is as of the writing of this (June 2006) no definitive treatise of the theory of KMC, but Fichthorn and Weinberg have discussed the theory for thermodynamic equilibrium KMC simulations in detail in (Fichthorn 1991). A good introduction is given also by Art Voter (Voter 2005),http://www.ipam.ucla.edu/publications/matut/matut_5898_preprint.pdf and by A.P.J. Jansen (Jansen 2003),http://arxiv.org/abs/cond-mat/0303028,
and a recent review is (Chatterjee 2007) or (Chotia 2008).
In March, 2006 the, probably, first commercial software using Kinetic Monte Carlo to simulate the diffusion and activation/deactivation of dopants in Silicon and Silicon-like materials is released by Synopsys
Synopsys
Synopsys, Inc. is one of the largest companies in the Electronic Design Automation industry. Synopsys' first and best-known product is Design Compiler, a logic-synthesis tool. Synopsys offers a wide range of other products used in the design of an application-specific integrated circuit...
, reported by Martin-Bragado et al. (Martin-Bragado 06).
Varieties of KMC
The KMC method can be subdivided by how the objects are moving or reactionsoccurring. At least the following subdivisions are used:
- Lattice KMC (LKMC) signifies KMC carried out on an atomic latticeCrystal structureIn mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. Often this variety is also called atomistic KMC, (AKMC). A typical example is simulation of vacancy diffusionDiffusionMolecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
in alloyAlloyAn alloy is a mixture or metallic solid solution composed of two or more elements. Complete solid solution alloys give single solid phase microstructure, while partial solutions give two or more phases that may or may not be homogeneous in distribution, depending on thermal history...
s, where a vacancy is allowed to jump around the lattice with rates that depend on the local elemental composition
- Object KMC (OKMC) means KMC carried out for defectsCrystallographic defectCrystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...
or impuritiesImpurityImpurities are substances inside a confined amount of liquid, gas, or solid, which differ from the chemical composition of the material or compound.Impurities are either naturally occurring or added during synthesis of a chemical or commercial product...
, which are jumping either in random or lattice-specific directions. Only the positions of the jumping objects are included in the simulation, not those of the 'background' lattice atoms. The basic KMC step is one object jump.
- Event KMC (EKMC) or First-passage KMC (FPKMC) signifies an OKMC variety where the following reaction between objects (e.g. clustering of two impuritiesImpurityImpurities are substances inside a confined amount of liquid, gas, or solid, which differ from the chemical composition of the material or compound.Impurities are either naturally occurring or added during synthesis of a chemical or commercial product...
or vacancy-interstitialInterstitial defectInterstitials are a variety of crystallographic defects, i.e. atoms which occupy a site in the crystal structure at which there is usually not an atom, or two or more atoms sharing one or more lattice sites such that the number of atoms is larger than the number of lattice sites.They are generally...
annihilation) is chosen with the KMC algorithm, taking the object positions into account, and this event is then immediately carried out (Dalla Torre 2005, Oppelstrup 2006).