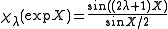Kirillov character formula
Encyclopedia
In mathematics
, for a Lie group
 , the Kirillov orbit method gives a heuristic method in representation theory
, the Kirillov orbit method gives a heuristic method in representation theory
. It connects the Fourier transform
s of coadjoint orbits, which lie in the dual space
of the Lie algebra
of G, to the infinitesimal character
s of the irreducible representations. The method got its name after the Russia
n mathematician Alexandre Kirillov
.
At its simplest, it states that a character of a Lie group may be given by the Fourier transform
of the Dirac delta function
support
ed on the coadjoint orbits, weighted by the square-root of the Jacobian
of the exponential map
, denoted by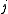 . It does not apply to all Lie groups, but works for a number of classes of connected
. It does not apply to all Lie groups, but works for a number of classes of connected
Lie groups, including nilpotent
, some semisimple groups, and compact group
s.
The Kirillov orbit method has led to a number of important developments in Lie theory, including the Duflo isomorphism and the wrapping map.
 be the highest weight of an irreducible representation
be the highest weight of an irreducible representation
in the dual
of the lie algebra
of the maximal torus
, denoted by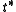 , and
, and 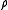 the half sum of the roots.
the half sum of the roots.
We denote by
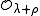
the coadjoint orbit through
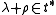
and
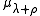
is the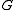 -invariant measure
-invariant measure
on

with total mass
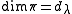 ,
,
known as the Liouville measure. If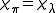 is the character of a representation
is the character of a representation
, then Kirillov's character formula for compact Lie groups is then given by
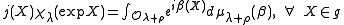
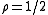 . The coadjoint orbits are the two-dimensional spheres
. The coadjoint orbits are the two-dimensional spheres
of radius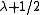 , centered at the origin in 3-dimensional space.
, centered at the origin in 3-dimensional space.
By the theory of Bessel function
s, it may be shown that
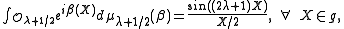
and
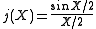
thus yielding the characters of SU(2):
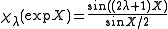
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, for a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
 , the Kirillov orbit method gives a heuristic method in representation theory
, the Kirillov orbit method gives a heuristic method in representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. It connects the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s of coadjoint orbits, which lie in the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G, to the infinitesimal character
Infinitesimal character
In mathematics, the infinitesimal character of an irreducible representation ρ of a semisimple Lie group G on a vector space V is, roughly speaking, a mapping to scalars that encodes the process of first differentiating and then diagonalizing the representation...
s of the irreducible representations. The method got its name after the Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician Alexandre Kirillov
Alexandre Kirillov
Alexandre Aleksandrovich Kirillov is a Soviet and Russian mathematician, renowned for his works in the fields of representation theory, topological groups and Lie groups. In particular he introduced the orbit method into representation theory....
.
At its simplest, it states that a character of a Lie group may be given by the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
ed on the coadjoint orbits, weighted by the square-root of the Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
, denoted by
 . It does not apply to all Lie groups, but works for a number of classes of connected
. It does not apply to all Lie groups, but works for a number of classes of connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
Lie groups, including nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
, some semisimple groups, and compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s.
The Kirillov orbit method has led to a number of important developments in Lie theory, including the Duflo isomorphism and the wrapping map.
Character formula for compact Lie groups
Let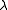 be the highest weight of an irreducible representation
be the highest weight of an irreducible representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
in the dual
Dual
Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...
of the lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of the maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
, denoted by
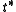 , and
, and 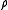 the half sum of the roots.
the half sum of the roots.We denote by
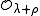
the coadjoint orbit through
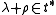
and
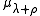
is the
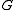 -invariant measure
-invariant measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on

with total mass
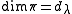 ,
,known as the Liouville measure. If
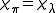 is the character of a representation
is the character of a representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
, then Kirillov's character formula for compact Lie groups is then given by
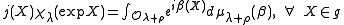
Example: SU(2)
For the case of SU(2), the highest weights are the positive half integers, and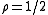 . The coadjoint orbits are the two-dimensional spheres
. The coadjoint orbits are the two-dimensional spheresSPHERES
The Synchronized Position Hold, Engage, Reorient Experimental Satellites experiment is a testbed consisting of three miniaturized satellites that can operate in a variety of environments, including inside the International Space Station...
of radius
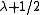 , centered at the origin in 3-dimensional space.
, centered at the origin in 3-dimensional space.By the theory of Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s, it may be shown that
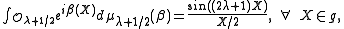
and
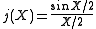
thus yielding the characters of SU(2):