Klee–Minty cube - AbsoluteAstronomy.com

The Klee–Minty cube is a unit cube

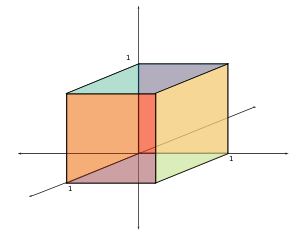
Unit cube

A unit cube, sometimes called a cube of side 1, is a cube whose sides are 1 unit long. The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units.- Unit Hypercube :...

whose corners have been slightly perturbed. Klee and Minty demonstrated that Dantzig's simplex algorithm

Simplex algorithm

In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....

has poor worst-case performance when initialized at one corner of their "squashed cube".

In particular, many optimization algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

s for linear optimization

Linear programming

Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...

exhibit poor performance when applied to the Klee–Minty cube. In 1973 Klee and Minty showed that Dantzig's simplex algorithm

Simplex algorithm

was not a polynomial-time algorithm when applied to their cube. Later, modifications of the Klee–Minty cube have shown poor behavior both for other basis

Matroid

In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....

-exchange pivoting algorithms and also for interior-point algorithms.

Description of the cube

The Klee–Minty cube was originally specified with a parameterized system of linear inequalities, with the dimension as the parameter. When the dimension is two, the "cube" is a squashed square. When the dimension is three, the "cube" is a squashed cube. Illustrations of the "cube" have appeared besides algebraic descriptions.

Computational complexity

The Klee–Minty cube has been used to analyze the performance of many algorithms, both in the worst case and on average. The time complexity

Time complexity

In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...

of an algorithm

Algorithm

counts the number of arithmetic operations sufficient for the algorithm to solve the problem. For example, Gaussian elimination

Gaussian elimination

In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...

requires on the order of D³ operations, and so it is said to have polynomial time-complexity, because its complexity is bounded by a cubic polynomial. There are examples of algorithms that do not have polynomial-time complexity. For example, a generalization of Gaussian elimination called Buchberger's algorithm

Buchberger's algorithm

In computational algebraic geometry and computational commutative algebra, Buchberger's algorithm is a method of transforming a given set of generators for a polynomial ideal into a Gröbner basis with respect to some monomial order. It was invented by Austrian mathematician Bruno Buchberger...

has for its complexity an exponential function of the problem data (the degree of the polynomial

Degree of a polynomial

The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...

s and the number of variables of the multivariate polynomials). Because exponential functions eventually grow much faster than polynomial functions, an exponential complexity implies that an algorithm has slow performance on large problems.

Worst case

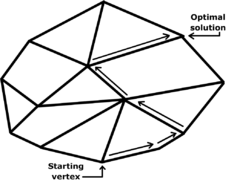
In mathematical optimization, the Klee–Minty cube is an example that shows the worst-case computational

Computational Complexity

Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...

complexity

Time complexity

of many algorithm

Algorithm

s of linear optimization. It is a deformed cube

Unit cube

with exactly 2^D corners in dimension

Dimension (vector space)

In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...

D. Klee and Minty showed that the Dantzig's

George Dantzig

George Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....

simplex algorithm

Simplex algorithm

visits all of a (perturbed) cube

Unit cube

in dimension D in the worst case.

Modifications of the Klee–Minty construction showed similar exponential time complexity

Time complexity

for other pivoting rules of simplex type, which maintain primal feasibility, such as Bland's rule

Bland's rule

In mathematical optimization, Bland's rule is an algorithmic refinement of the simplex method for linear optimization....

. Another modification showed that the criss-cross algorithm

Criss-cross algorithm

In mathematical optimization, the criss-cross algorithm denotes a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for...

, which does not maintain primal feasibility, also visits all the corners of a modified Klee–Minty cube. Like the simplex algorithm, the criss-cross algorithm visits all 8 corners of the three-dimensional cube in the worst case.

Path-following algorithms

Further modifications of the Klee–Minty cube have shown poor performance of central-path–following algorithms for linear optimization, in that the central path comes arbitrarily close to each of the corners of a cube. This "vertex-stalking" performance is surprising, because such path-following algorithms have polynomial-time complexity for linear optimization.

Average case

The Klee–Minty cube has also inspired research on average-case complexity

Average-case complexity

Average-case complexity is a subfield of computational complexity theory that studies the complexity of algorithms on random inputs.The study of average-case complexity has applications in the theory of cryptography....

. When eligible pivots are made randomly (and not by the rule of steepest descent), Dantzig's simplex algorithm needs on average

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

quadratically

Quadratic polynomial

In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...

many steps (on the order of O(D²).
Standard variants of the simplex algorithm takes on average D steps for a cube. When it is initialized at a random corner of the cube, the criss-cross algorithm visits only D additional corners, however, according to a 1994 paper by Fukuda and Namiki. Both the simplex algorithm and the criss-cross algorithm visit exactly 3 additional corners of the three-dimensional cube on average.

Description of the cube

Computational complexity

Worst case

Path-following algorithms

Average case

See also

Algebraic description with illustration

System of linear inequalities with no picture

Pictures with no linear system