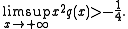Kneser theorem
Encyclopedia
In mathematics
, in the field of ordinary differential equation
s, the Kneser theorem, named after Adolf Kneser
, provides criteria to decide whether a differential equation is oscillating or not.
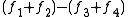
with
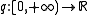
continuous
.
We say this equation is oscillating if it has a solution y with infinitely many zeros, and non-oscillating otherwise.
The theorem states that the equation is non-oscillating if
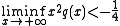
and oscillating if
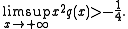
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, the Kneser theorem, named after Adolf Kneser
Adolf Kneser
Adolf Kneser was a German mathematician.He was born in Grüssow, Mecklenburg, Germany and died in Breslau, Germany ....
, provides criteria to decide whether a differential equation is oscillating or not.
Statement of the theorem
Consider an ordinary linear homogenous differential equation of the form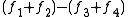
with
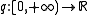
continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
We say this equation is oscillating if it has a solution y with infinitely many zeros, and non-oscillating otherwise.
The theorem states that the equation is non-oscillating if
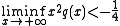
and oscillating if