
Knot thickness
Encyclopedia
In knot theory
, each link and knot can have an assigned knot thickness. Each realization of a link or knot has a thickness assigned to it. The thickness τ of a link allows us to introduce a scale with respect to which we can then define the ropelength
of a link.
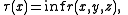
where x, y, and z are points on the link, all distinct, and r(x, y, z) is the radius of the circle that passes through all three points (x, y, z). From this definition we can deduce that the local thickness is at most equal to the local radius of curvature.
The thickness of a link is defined as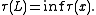
to the link with radius equal to τ(L) will not self intersect, and so we arrive at a "real world" knot made out of a thick string.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, each link and knot can have an assigned knot thickness. Each realization of a link or knot has a thickness assigned to it. The thickness τ of a link allows us to introduce a scale with respect to which we can then define the ropelength
Ropelength
In knot theory each realization of a link or knot has an associated ropelength. Intuitively this is the minimal length of an ideally flexible rope that is needed to tie a given link, or knot...
of a link.
Definition
There exist several possible definitions of thickness that coincide for smooth enough curves.Global Radius of Curvature
The thickness is defined using the simpler concept of the local thickness τ(x). The local thickness at a point x on the link is defined as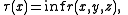
where x, y, and z are points on the link, all distinct, and r(x, y, z) is the radius of the circle that passes through all three points (x, y, z). From this definition we can deduce that the local thickness is at most equal to the local radius of curvature.
The thickness of a link is defined as
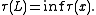
Injectivity Radius
This definition ensures that a normal tubeNormal tube
In topology, a normal tube to a smooth curve is a manifold defined as the union of all discs such that* all the discs have the same fixed radius;* the center of each disc lies on the curve; and...
to the link with radius equal to τ(L) will not self intersect, and so we arrive at a "real world" knot made out of a thick string.

