Ropelength
Encyclopedia
In knot theory
each realization of a link or knot has an associated ropelength. Intuitively this is the minimal length of an ideally flexible rope that is needed to tie a given link, or knot. Knots and links that minimize ropelength are called ideal knots and ideal links respectively.
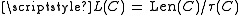, where Len(C) is the length of C and τ(C) is the thickness
of the link defined by C.
In our terms we are asking if there is a knot with ropelength 12. This question has been answered, and it was shown to be impossible: the ropelength of any nontrivial knot has to be at least 15.66. However, the search for the answer has spurred a lot of research on both theoretical and computational ground. It has been shown that for each link type there is a ropelength minimizer although it is only of class C 1, 1. For the simplest nontrivial knot, the trefoil knot, computer simulations have shown that its ropelength is at most 16.372.
of a knot. It has been shown that
and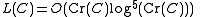
for a knot C with crossing number Cr(C) and ropelength L(C), where the O and Ω are examples of big O notation
and big Omega notation, respectively.
The lower bound (big Omega) is shown with two families ((k, k−1) torus knots and k-Hopf links) that realize this bound. A former upper bound of O(Cr(C))3/2 has been shown using Hamiltonian cycles in graphs embedded in a cubic integer lattice. The current best near-linear upper bound was established with a divide-and-conquer argument to show that minimum projections of knots can be embedded as planar graphs in the cubic lattice. However, no one has yet observed a knot family with super-linear length dependence L(C) > O(Cr(CK)) and it is conjectured that the upper bound is in fact linear.
by defining the ropelength of a knot type to be the minimum ropelength over all realizations of that knot type. So far this invariant is impractical as we have not determined that minimum for the majority of knots.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
each realization of a link or knot has an associated ropelength. Intuitively this is the minimal length of an ideally flexible rope that is needed to tie a given link, or knot. Knots and links that minimize ropelength are called ideal knots and ideal links respectively.
Definition
The ropelength of a knot curve C is defined as the ratio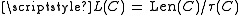, where Len(C) is the length of C and τ(C) is the thicknessKnot thickness
In knot theory, each link and knot can have an assigned knot thickness. Each realization of a link or knot has a thickness assigned to it. The thickness τ of a link allows us to introduce a scale with respect to which we can then define the ropelength of a link....
of the link defined by C.
Ropelength minimizers
One of the earliest knot theory questions was posed in the following terms:
Can I tie a knot on a foot-long rope that is one inch thick?
In our terms we are asking if there is a knot with ropelength 12. This question has been answered, and it was shown to be impossible: the ropelength of any nontrivial knot has to be at least 15.66. However, the search for the answer has spurred a lot of research on both theoretical and computational ground. It has been shown that for each link type there is a ropelength minimizer although it is only of class C 1, 1. For the simplest nontrivial knot, the trefoil knot, computer simulations have shown that its ropelength is at most 16.372.
Dependence of ropelength on other knot invariants
An extensive search has been devoted to showing relations between ropelength and other knot invariants. As an example there are well known bounds on the asymptotic dependence of ropelength on the crossing numberCrossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
of a knot. It has been shown that
and
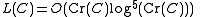
for a knot C with crossing number Cr(C) and ropelength L(C), where the O and Ω are examples of big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
and big Omega notation, respectively.
The lower bound (big Omega) is shown with two families ((k, k−1) torus knots and k-Hopf links) that realize this bound. A former upper bound of O(Cr(C))3/2 has been shown using Hamiltonian cycles in graphs embedded in a cubic integer lattice. The current best near-linear upper bound was established with a divide-and-conquer argument to show that minimum projections of knots can be embedded as planar graphs in the cubic lattice. However, no one has yet observed a knot family with super-linear length dependence L(C) > O(Cr(CK)) and it is conjectured that the upper bound is in fact linear.
Ropelength as a knot invariant
Ropelength can be turned into a knot invariantKnot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
by defining the ropelength of a knot type to be the minimum ropelength over all realizations of that knot type. So far this invariant is impractical as we have not determined that minimum for the majority of knots.