In mathematical psychology

Mathematical psychology

Mathematical psychology is an approach to psychological research that is based on mathematical modeling of perceptual, cognitive and motor processes, and on the establishment of law-like rules that relate quantifiable stimulus characteristics with quantifiable behavior...

, a knowledge space is a combinatorial structure

Antimatroid

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...

 describing the possible states of knowledge of a human learner.
To form a knowledge space, one models a domain of knowledge as a set of concepts, and a feasible state of knowledge as a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

 of that set containing the concepts known or knowable by some individual. Typically, not all subsets are feasible, due to prerequisite relations among the concepts. The knowledge space is the family of all the feasible subsets. Knowledge spaces were introduced in 1985 by Jean-Paul Doignon and Jean-Claude Falmagne

Jean-Claude Falmagne

Jean-Claude Falmagne is a mathematical psychologist whose scientific contributions deal with problems in reaction time theory, psychophysics, philosophy of science, measurement theory, decision theory, and educational technology...

 and have since been studied by many other researchers. They also form the basis for two computerized tutoring systems, RATH and ALEKS

Aleks

ALEKS is an Internet based interactive mathematics and science tutoring and assessment program for subjects in mathematics, the sciences, and business....

.

It is possible to interpret a knowledge space as a special form of a restricted latent class model.

Definitions

Some basic definitions used in the knowledge space approach -

• A tuple 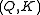consisting of a non-empty set 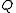and a set 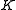of subsets from is called a knowledge structure if 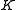contains the empty set and .
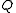• A knowledge structure is called a knowledge space if it is closed under union, i.e. if implies .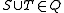
• A knowledge space is called a quasi-ordinal knowledge space if it is in addition closed under intersection, i.e. if implies 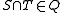. Closure under both unions and intersections gives (Q,∪,∩) the structure of a distributive lattice
  Distributive lattice
  In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
  
  ; Birkhoff's representation theorem
  Birkhoff's representation theorem
  In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets...
  
   for distributive lattices shows that there is a one-to-one correspondence between the set of all quasiorders
  Preorder
  In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
  
   on Q and the set of all quasi-ordinal knowledge spaces on Q. I.e., each quasi-ordinal knowledge space can be represented by a quasi-order and vice versa.

An important subclass of knowledge spaces, the well-graded knowledge spaces or learning spaces, can be defined as satisfying two additional mathematical axioms:

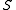1. If and 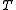are both feasible subsets of concepts, then 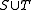is also feasible. In educational terms: if it is possible for someone to know all the concepts in S, and someone else to know all the concepts in T, then we can posit the potential existence of a third person who combines the knowledge of both people.
2. If 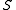is a nonempty feasible subset of concepts, then there is some concept x in S such that 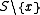is also feasible. In educational terms: any feasible state of knowledge can be reached by learning one concept at a time.

A set family satisfying these two axioms forms a mathematical structure

Mathematical structure

In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....

 known as an antimatroid

Antimatroid

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...

.

Construction of knowledge spaces

In practice there exist several methods to construct knowledge spaces. The most frequently used method is querying experts. There exist several querying algorithms that allow one or several experts to construct a knowledge space by answering a sequence of simple questions.

Another method is to construct the knowledge space by explorative data analysis (for example by Item tree analysis

Item tree analysis

Item tree analysis is a data analytical method which allows constructing ahierarchical structure on the items of a questionnaire or test from observed responsepatterns. Assume that we have a questionnaire with m items and that subjects can...

) from data.
A third method is to derive the knowledge space from an analysis of the problem solving processes in the corresponding domain.