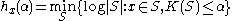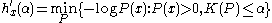Kolmogorov structure function
Encyclopedia
In 1974 Kolmogorov proposed a non-probabilistic approach to statistics and model selection. Let each data be a finite binary string and models be finite sets of binary strings. Consider model classes consisting of models of given maximal Kolmogorov complexity
.
The Kolmogorov Structure function of an individual data string expresses the relation between the complexity level constraint on a model class and the least log-cardinality of a model in the class containing the data. The structure function determines all stochastic
properties of the individual data string: for every constrained model class it determines the individual best-fitting model in the class irrespective of whether the true model is in the model class considered or not. In the classical case we talk about a set of data with a probability distribution, and the properties are those of the expectations. In contrast, here we deal with individual data strings and the properties of the individual string focussed on. In this setting, a property holds with certainty rather than with high probability as in the classical case. The Kolmogorov Structure function precisely quantify the goodness-of-fit of an individual model with respect to individual data.
The Kolmogorov Structure function is used in the algorithmic information theory
, also known as the theory of Kolmogorov complexity
, for describing the structure of a string
by use of model
s of increasing complexity.
The structure function was originally proposed by Kolmogorov in 1973 at a Soviet Information Theory symposium in Tallinn, but these results were not published p.182. But the results were announced in in 1974, the only written record by Kolmogorov himself. One of his last scientific statements is (translated from the original Russian by L.A. Levin):
The Kolmogorov Structure function can be written as
where x is a binary string of length n with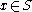
where S is a contemplated model (set of n-length strings) for x, 
is the Kolmogorov complexity
of S and
is a nonnegative integer value bounding the complexity of the contemplated S's. Clearly, this function is nonincreasing and reaches 
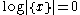for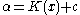 
where c is the required number of bits to change x into 
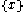and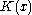 
is the Kolmogorov complexity
of x.
.
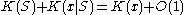The function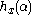
never decreases more than a fixed independent constant below the diagonal called sufficiency line L defined by
.
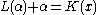It is approached to within a constant distance by the graph of
for certain arguments (for instance, for 
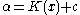). For these 
's we have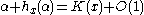 
and the associated model S (witness for 
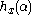) is called an optimal set for $x$, and its description of 
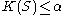bits is therefore an algorithmic sufficient statistic. We write `algorithmic' for `Kolmogorov complexity' by convention. The main properties of an algorithmic sufficient statistic are the following: If S is an algorithmic sufficient statistic for x, then
.
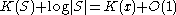That is, the two-part description of x using the model S and as data-to-model code the index of x in the enumeration of S in
bits, is as concise as the shortest one-part code of x in 
bits. This can be easily seen as follows: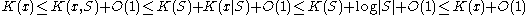
,
using straightforward inequalities and the sufficiency property, we find that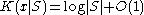
. (For example, given 
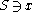, we can describe x self-delimitingly (you can determine its end) in 
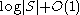bits.) Therefore, the randomness deficiency 
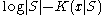of x in S is a constant, which means that x is a typical
(random) element of S. However, there can be models S containing x that are not sufficient statistics. An algorithmic sufficient statistic S for x has the additional property, apart from being a model of best fit, that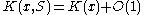
and therefore by the Kolmogorov complexity symmetry of information (the information about x in S is about the same as the information about S in x) we have 
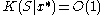: the algorithmic sufficient statistic S is a model of best fit that is almost completely determined by x. (
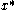is a shortest program for x.) The algorithmic sufficient statistic associated with the least such 
is called the algorithmic minimal sufficient statistic.
With respect to the picture: The MDL Structure function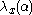
is explained below. The Goodness-of-fit Structure function 
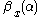is the least randomness deficiency (see above) of any model 
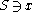for x such that 
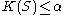. This structure function gives the goodness-of-fit of a model S (containing x) for the string x. When it is low the model fits well, and when it is high the model doesn't fit well. If 
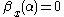for some 
then there is a typical model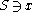 
for x such that 
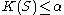and x is typical (random) for S. That is, S is the best-fitting model for x. For more details see and especially and .
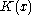, every graph (up to a 
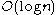additive term in argument and value) is realized by the structure function of some data x and vice versa. Where the graph hits the diagonal first the argument (complexity) is that of the minimum sufficient statistic. It is incomputable to determine this place. See .
of complexity the structure function allows us to select the best model S for the individual string x within a strip of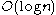 
with certainty, not with great probability .
(MDL) function: The length of the minimal two-part code for x consisting of the model cost K(S) and the
length of the index of x in S, in the model class of sets of given maximal Kolmogorov complexity
, the complexity of S upper bounded by 
, is given by the MDL function or constrained MDL estimator:
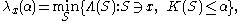
where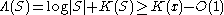
is the total length of two-part code of x with help of model S.
of complexity the structure function allows us to select the best model S for the individual string x within a strip of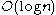 
with certainty, not with great probability .
by its inventor Jorma Rissanen
.
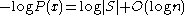. For example, if P is the uniform distribution on the set S of strings of length n, then each 
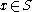has probability 
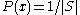. In the general case of computable probability mass functions we incur a logarithmic additive error term. Kolmogorov's Structure function becomes
where x is a binary string of length n with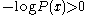
where P is a contemplated model (computable probability of n-length strings) for x, 
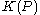is the Kolmogorov complexity
of P and
is a integer value bounding the complexity of the contemplated P's. Clearly, this function is nonincreasing and reaches 
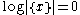for 
where c is the required number of bits to change x into 
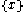and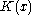 
is the Kolmogorov complexity
of x. Then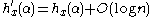
. For every complexity level 
the function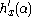 
is the Kolmogorov complexity version of the maximum likelihood
(ML).
of complexity the structure function allows us to select the best model S for the individual string x within a strip of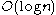 
with certainty, not with great probability.
length of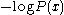
, in the model class of computable probability mass functions of given maximal Kolmogorov complexity 
, the complexity of P upper bounded by 
, is given bythe MDL function or constrained MDL estimator:
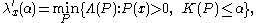
where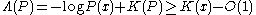
is the total length of two-part code of x with help of model P.
of complexity the MDL function allows us to select the best model P for the individual string x within a strip of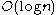 
with certainty, not with great probability .
and denoising of individual finite sequences using Kolmogorov complexity. Experiments using real compressor programs have been carried out with success . Here the assumption is that for natural data the Kolmogorov complexity is not far from the length of a compressed version using a good compressor.
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
.
The Kolmogorov Structure function of an individual data string expresses the relation between the complexity level constraint on a model class and the least log-cardinality of a model in the class containing the data. The structure function determines all stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
properties of the individual data string: for every constrained model class it determines the individual best-fitting model in the class irrespective of whether the true model is in the model class considered or not. In the classical case we talk about a set of data with a probability distribution, and the properties are those of the expectations. In contrast, here we deal with individual data strings and the properties of the individual string focussed on. In this setting, a property holds with certainty rather than with high probability as in the classical case. The Kolmogorov Structure function precisely quantify the goodness-of-fit of an individual model with respect to individual data.
The Kolmogorov Structure function is used in the algorithmic information theory
Algorithmic information theory
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
, also known as the theory of Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
, for describing the structure of a string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
by use of model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s of increasing complexity.
Kolmogorov's definition
"To each constructive object corresponds a functionof a
natural number k---the log of minimal cardinality of x-containing
sets that allow definitions of complexity at most k.
If the element x itself allows a simple definition,
then the functiondrops to 0 even for small k.
Lacking such definition, the element is "random" in a negative sense.
But it is positively "probabilistically random" only when function
having taken the value
at a relatively small
, then changes approximately as
.
[Kolmogorov, in the announcement cited above]
Contemporary definition
It is discussed in . It is extensively studied in where also the main properties are resolved.The Kolmogorov Structure function can be written as
where x is a binary string of length n with
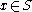where S is a contemplated model (set of n-length strings) for x, is the Kolmogorov complexityKolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
of S and
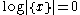is a nonnegative integer value bounding the complexity of the contemplated S's. Clearly, this function is nonincreasing and reaches for 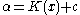where c is the required number of bits to change x into 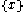and 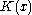is the Kolmogorov complexityKolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
of x.
The algorithmic sufficient statistic
We define a set S containing x such that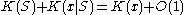.The function
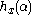never decreases more than a fixed independent constant below the diagonal called sufficiency line L defined by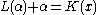.It is approached to within a constant distance by the graph of
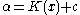for certain arguments (for instance, for ). For these 's we have 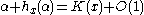and the associated model S (witness for 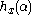) is called an optimal set for $x$, and its description of 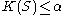bits is therefore an algorithmic sufficient statistic. We write `algorithmic' for `Kolmogorov complexity' by convention. The main properties of an algorithmic sufficient statistic are the following: If S is an algorithmic sufficient statistic for x, then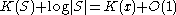.That is, the two-part description of x using the model S and as data-to-model code the index of x in the enumeration of S in
bits, is as concise as the shortest one-part code of x in bits. This can be easily seen as follows: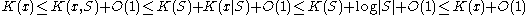,using straightforward inequalities and the sufficiency property, we find that
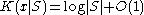. (For example, given 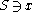, we can describe x self-delimitingly (you can determine its end) in 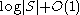bits.) Therefore, the randomness deficiency 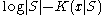of x in S is a constant, which means that x is a typicalTypical
"Typical" is the Grammy Award nominated debut single from New Orleans rock group Mutemath. The song was written in 2003 by Paul Meany and Darren King. The digital single was released on April 10, 2007. A physical single was released in the UK only on August 27, 2007. Josh Harris club remixes of the...
(random) element of S. However, there can be models S containing x that are not sufficient statistics. An algorithmic sufficient statistic S for x has the additional property, apart from being a model of best fit, that
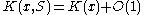and therefore by the Kolmogorov complexity symmetry of information (the information about x in S is about the same as the information about S in x) we have 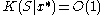: the algorithmic sufficient statistic S is a model of best fit that is almost completely determined by x. ( 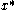is a shortest program for x.) The algorithmic sufficient statistic associated with the least such is called the algorithmic minimal sufficient statistic.With respect to the picture: The MDL Structure function
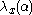is explained below. The Goodness-of-fit Structure function 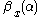is the least randomness deficiency (see above) of any model 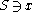for x such that 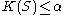. This structure function gives the goodness-of-fit of a model S (containing x) for the string x. When it is low the model fits well, and when it is high the model doesn't fit well. If 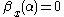for some then there is a typical model 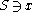for x such that 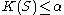and x is typical (random) for S. That is, S is the best-fitting model for x. For more details see and especially and .Selection of properties
Within the constraints that the graph goes down at an angle of at least 45 degrees, that it starts at n and ends approximately at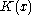, every graph (up to a 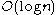additive term in argument and value) is realized by the structure function of some data x and vice versa. Where the graph hits the diagonal first the argument (complexity) is that of the minimum sufficient statistic. It is incomputable to determine this place. See .Main property
It is proved that at each level of complexity the structure function allows us to select the best model S for the individual string x within a strip of 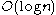with certainty, not with great probability .The MDL variant
The Minimum description lengthMinimum description length
The minimum description length principle is a formalization of Occam's Razor in which the best hypothesis for a given set of data is the one that leads to the best compression of the data. MDL was introduced by Jorma Rissanen in 1978...
(MDL) function: The length of the minimal two-part code for x consisting of the model cost K(S) and the
length of the index of x in S, in the model class of sets of given maximal Kolmogorov complexity
, the complexity of S upper bounded by , is given by the MDL function or constrained MDL estimator: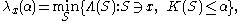where
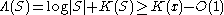is the total length of two-part code of x with help of model S.Main property
It is proved that at each level of complexity the structure function allows us to select the best model S for the individual string x within a strip of 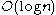with certainty, not with great probability .Application in statistics
The mathematics developed above were taken as the foundation of MDLMDL
MDL may mean:* Mazagon Dock Limited, an Indian shipyard* MdL , an American music producer* MDL , a biochemical compound* MDL , a derivative of the LISP language...
by its inventor Jorma Rissanen
Jorma Rissanen
Jorma J. Rissanen is an information theorist, known for inventing the arithmetic coding technique of lossless data compression, and the minimum description length principle....
.
Probability models and the Kolmogorov structure function
For every computable probability distribution P it can be proved that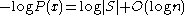. For example, if P is the uniform distribution on the set S of strings of length n, then each 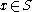has probability 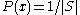. In the general case of computable probability mass functions we incur a logarithmic additive error term. Kolmogorov's Structure function becomes
where x is a binary string of length n with
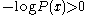where P is a contemplated model (computable probability of n-length strings) for x, 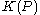is the Kolmogorov complexityKolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
of P and
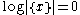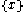is a integer value bounding the complexity of the contemplated P's. Clearly, this function is nonincreasing and reaches for where c is the required number of bits to change x into and 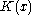is the Kolmogorov complexityKolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
of x. Then
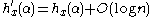. For every complexity level the function 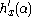is the Kolmogorov complexity version of the maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
(ML).
Main property
It is proved that at each level of complexity the structure function allows us to select the best model S for the individual string x within a strip of 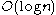with certainty, not with great probability.The MDL Variant and probability models
The MDL function: The length of the minimal two-part code for x consisting of the model cost K(P) and thelength of
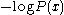, in the model class of computable probability mass functions of given maximal Kolmogorov complexity , the complexity of P upper bounded by , is given bythe MDL function or constrained MDL estimator: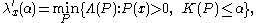where
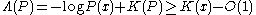is the total length of two-part code of x with help of model P.Main property
It is proved that at each level of complexity the MDL function allows us to select the best model P for the individual string x within a strip of 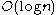with certainty, not with great probability .Extension to rate distortion and denoising
It turns out that the approach can be extended to a theory of rate distortion of individual finite sequencesand denoising of individual finite sequences using Kolmogorov complexity. Experiments using real compressor programs have been carried out with success . Here the assumption is that for natural data the Kolmogorov complexity is not far from the length of a compressed version using a good compressor.
Other Literature
- T.M. Cover, P. Gacs, R.M. Gray, Kolmogorov's contributions to Iinformation Theory and Algorithmic Complexity, Annals of Probability, 17:3(1989), 840-865.
- A. N. Kolmogorov and V. A. Uspensky. Algorithms and randomness, SIAM J. Theory of Probability and Its Applications, vol. 32 (1987), pp. 389-412.
- M. Li and P.M.B. Vitanyi, An Introduction to Kolmogorov Complexity and its Applications, Third Edition, Springer-Verlag, New York, 2008. Especially pp. 401-431 about the Kolmogorov Structure function, and pp. 613-629 about rate distortion and denoising of individual sequences.
- A.Kh. Shen, Discussion on Kolmogorov Complexity and Statistical Analysis, The Computer Journal (1999) 42(4): 340-342.
- V.V. V'yugin, On Randomness Defect of a Finite Object Relative to Measures with Given Complexity Bounds, Teor. Veroyatnost. i Primenen., 32:3 (1987), 558–563 (English translation in Theory of Probability and its Applications, 1987, 32:3, 508–512.)
- V.V. V'yugin, Algorithmic Complexity and Stochastic Properties of Finite Binary Sequences, The Computer Journal (1999) 42(4): 294-317.