Kolmogorov’s generalized criterion
Encyclopedia
Kolmogorov's
generalized criterion is a proposition
relating to continuous-time Markov processes which states that a stationary Markov process with state space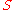
and generator matrix (transition rate matrix) 
has a reversed process with generator matrix 
if and only if:
This is a generalization of Kolmogorov’s criterion
which applies to Markov chain
s.
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
generalized criterion is a proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
relating to continuous-time Markov processes which states that a stationary Markov process with state space
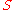and generator matrix (transition rate matrix) has a reversed process with generator matrix if and only if:-
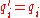for every state 
(where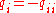 
). - For every finite sequence of states
, with n≥2, the condition
-
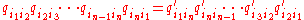holds.
This is a generalization of Kolmogorov’s criterion
Kolmogorov’s criterion
In probability theory, Kolmogorov's criterion, named after Andrey Kolmogorov, is a theorem in Markov processes concerning stationary Markov chains...
which applies to Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s.