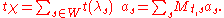Kostant polynomial
Encyclopedia
In mathematics
, the Kostant polynomials, named after Bertram Kostant
, provide an explicit basis of the ring of polynomials over the ring of polynomials invariant under the finite reflection group of a root system
.
of a compact semisimple group K with maximal torus T, then the Kostant polynomials describe the structure of the de Rham cohomology
of the generalized flag manifold
K/T, also isomorphic to G/B where G is the complexification of K and B is the corresponding Borel subgroup
. Armand Borel
showed that its cohomology ring is isomorphic to the quotient of the ring of polynomials by the ideal generated by the invariant homogeneous polynomials of positive degree. This ring had already been considered by Claude Chevalley
in establishing the foundations of the cohomology of compact Lie groups and their homogeneous spaces with André Weil
, Jean-Louis Koszul
and Henri Cartan
; the existence of such a basis was used by Chevalley to prove that the ring of invariants was itself a polynomial ring. A detailed account of Kostant polynomials was given by and independently as a tool to understand the Schubert calculus
of the flag manifold. The Kostant polynomials are related to the Schubert polynomial
s defined combinatorially by for the classical flag manifold, when G = SL(n,C). Their structure is governed by difference operators associated to the corresponding root system
.
defined an analogous basis when the polynomial ring is replaced by the ring of exponentials of the weight lattice. If K is simply connected, this ring can be identified with the representation ring
R(T) and the W-invariant subring with R(K). Steinberg's basis was again motivated by a problem on the topology of homogeneous spaces; the basis arises in describing the T-equivariant K-theory of K/T.
in a finite-dimensional real inner product space V with Weyl group
W. Let Φ+ be a set of positive roots and Δ the corresponding set of simple roots. If α is a root, then sα denotes the corresponding reflection operator. Roots are regarded as linear polynomials on V using the inner product α(v) = (α,v). The choice of Δ gives rise to a Bruhat order
on the Weyl group
determined by the ways of writing elements minimally as products of simple root reflection. The minimal length for an elenet s is denoted
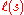. Pick an element v in V such that α(v) > 0 for every positive root.
If αi is a simple root with reflection operator si
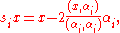
then the corresponding divided difference operator is defined by
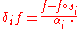
If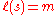
and s has reduced expression
then
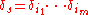
is independent of the reduced expression. Moreover
if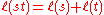
and 0 otherwise.
If w0 is the Coxeter element of W, the element of greatest length or equivalently the element sending Φ+ to
−Φ+, then
More generally
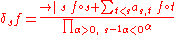
for some constants as,t.
Set
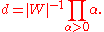
and
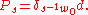
Then Ps is a homogeneous polynomial of degree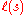
.
These polynomials are the Kostant polynomials.
In fact the matrix
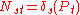
is unitriangular for any total order such that s ≥ t implies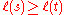
.
Hence
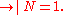
Thus if
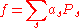
with as invariant under W, then
Thus
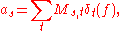
where
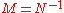
another unitriangular matrix with polynomial entries.
It can be checked directly that as is invariant under W.
In fact δi satisfies the derivation
property
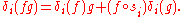
Hence
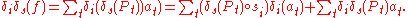
Since
or 0, it follows that
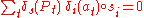
so that by the invertibility of N
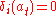
for all i, i.e. at is invariant under W.
in a real inner product space V, and Φ+ a subset of positive roots. From these data we obtain the subset Δ = { α1, α2, ..., αn} of the simple roots, the coroots
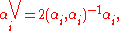
and the fundamental weights λ1, λ2, ..., λn as the dual basis of the coroots.
For each element s in W, let Δs be the subset of Δ consisting of the simple roots satisfying s−1α < 0, and put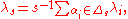
where the sum is calculated in the weight lattice P.
The set of linear combinations of the exponentials eμ with integer coefficients for μ in P becomes a ring over Z isomorphic to the group algebra of P, or equivalently to the representation ring
R(T) of T, where T is a maximal torus in K, the simply connected, connected compact semisimple Lie group with root system Φ. If W is the Weyl group of Φ, then the representation ring R(K) of K can be identified with R(T)W.
Steinberg's theorem. The exponentials λs (s in W) form a free basis for the ring of exponentials over the subring of W-invariant exponentials.
Let ρ denote the half sum of the positive roots, and A denote the antisymmetrisation operator
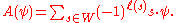
The positive roots β with sβ positive can be seen as a set of positive roots for a root system on a subspace of V; the roots are the ones orthogonal to s.λs. The corresponding Weyl group equals the stabilizer of λs in W. It is generated by the simple reflections sj for which sαj is a positive root.
Let M and N be the matrices
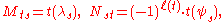
where ψs is given by the weight s−1ρ - λs. Then the matrix
is triangular with respect to any total order on W such that s ≥ t implies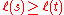
.
Steinberg proved that the entries of B are W-invariant exponential sums. Moreover its diagonal entries all equal 1, so it has determinant 1. Hence its inverse C has the same form. Define
If χ is an arbitrary exponential sum, then it follows that
with as the W-invariant exponential sum
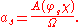
Indeed this is the unique solution of the system of equations
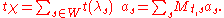
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Kostant polynomials, named after Bertram Kostant
Bertram Kostant
-Early life and education:Kostant grew up in New York City, where he graduated from the celebrated Stuyvesant High School in 1945. He went on to obtain an undergraduate degree in mathematics from Purdue University in 1950. He earned his Ph.D...
, provide an explicit basis of the ring of polynomials over the ring of polynomials invariant under the finite reflection group of a root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
.
Background
If the reflection group W corresponds to the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of a compact semisimple group K with maximal torus T, then the Kostant polynomials describe the structure of the de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
of the generalized flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
K/T, also isomorphic to G/B where G is the complexification of K and B is the corresponding Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
. Armand Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
showed that its cohomology ring is isomorphic to the quotient of the ring of polynomials by the ideal generated by the invariant homogeneous polynomials of positive degree. This ring had already been considered by Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
in establishing the foundations of the cohomology of compact Lie groups and their homogeneous spaces with André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, Jean-Louis Koszul
Jean-Louis Koszul
Jean-Louis Koszul is a mathematician best known for studying geometry and discovering the Koszul complex.He was educated at the Lycée Fustel-de-Coulanges in Strasbourg before studying at the Faculty of Science in Strasbourg and the Faculty of Science in Paris...
and Henri Cartan
Henri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
; the existence of such a basis was used by Chevalley to prove that the ring of invariants was itself a polynomial ring. A detailed account of Kostant polynomials was given by and independently as a tool to understand the Schubert calculus
Schubert calculus
In mathematics, Schubert calculus is a branch of algebraic geometry introduced in the nineteenth century by Hermann Schubert, in order to solve various counting problems of projective geometry...
of the flag manifold. The Kostant polynomials are related to the Schubert polynomial
Schubert polynomial
In mathematics, Schubert polynomials are generalizations of Schur polynomials that represent cohomology classes of Schubert cycles in flag varieties.They were introduced by and are named after Hermann Schubert.-Background:...
s defined combinatorially by for the classical flag manifold, when G = SL(n,C). Their structure is governed by difference operators associated to the corresponding root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
.
defined an analogous basis when the polynomial ring is replaced by the ring of exponentials of the weight lattice. If K is simply connected, this ring can be identified with the representation ring
Representation ring
In mathematics, especially in the area of algebra known as representation theory, the representation ring of a group is a ring formed from all the linear representations of the group. For a given group, the ring will depend on the base field of the representations...
R(T) and the W-invariant subring with R(K). Steinberg's basis was again motivated by a problem on the topology of homogeneous spaces; the basis arises in describing the T-equivariant K-theory of K/T.
Definition
Let Φ be a root systemRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
in a finite-dimensional real inner product space V with Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
W. Let Φ+ be a set of positive roots and Δ the corresponding set of simple roots. If α is a root, then sα denotes the corresponding reflection operator. Roots are regarded as linear polynomials on V using the inner product α(v) = (α,v). The choice of Δ gives rise to a Bruhat order
Bruhat order
In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
on the Weyl group
determined by the ways of writing elements minimally as products of simple root reflection. The minimal length for an elenet s is denoted
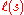. Pick an element v in V such that α(v) > 0 for every positive root.If αi is a simple root with reflection operator si
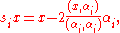
then the corresponding divided difference operator is defined by
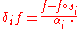
If
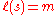and s has reduced expressionthen
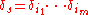
is independent of the reduced expression. Moreover
if
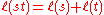and 0 otherwise.If w0 is the Coxeter element of W, the element of greatest length or equivalently the element sending Φ+ to
−Φ+, then
More generally
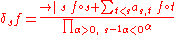
for some constants as,t.
Set
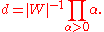
and
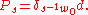
Then Ps is a homogeneous polynomial of degree
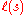.These polynomials are the Kostant polynomials.
Properties
Theorem. The Kostant polynomials form a free basis of the ring of polynomials over the W-invariant polynomials.In fact the matrix
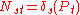
is unitriangular for any total order such that s ≥ t implies
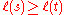.Hence
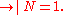
Thus if
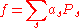
with as invariant under W, then
Thus
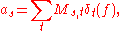
where
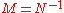
another unitriangular matrix with polynomial entries.
It can be checked directly that as is invariant under W.
In fact δi satisfies the derivation
Derivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
property
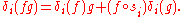
Hence
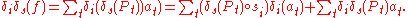
Since
or 0, it follows that
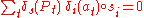
so that by the invertibility of N
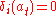
for all i, i.e. at is invariant under W.
Steinberg basis
As above let Φ be a root systemRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
in a real inner product space V, and Φ+ a subset of positive roots. From these data we obtain the subset Δ = { α1, α2, ..., αn} of the simple roots, the coroots
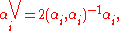
and the fundamental weights λ1, λ2, ..., λn as the dual basis of the coroots.
For each element s in W, let Δs be the subset of Δ consisting of the simple roots satisfying s−1α < 0, and put
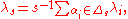
where the sum is calculated in the weight lattice P.
The set of linear combinations of the exponentials eμ with integer coefficients for μ in P becomes a ring over Z isomorphic to the group algebra of P, or equivalently to the representation ring
R(T) of T, where T is a maximal torus in K, the simply connected, connected compact semisimple Lie group with root system Φ. If W is the Weyl group of Φ, then the representation ring R(K) of K can be identified with R(T)W.
Steinberg's theorem. The exponentials λs (s in W) form a free basis for the ring of exponentials over the subring of W-invariant exponentials.
Let ρ denote the half sum of the positive roots, and A denote the antisymmetrisation operator
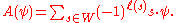
The positive roots β with sβ positive can be seen as a set of positive roots for a root system on a subspace of V; the roots are the ones orthogonal to s.λs. The corresponding Weyl group equals the stabilizer of λs in W. It is generated by the simple reflections sj for which sαj is a positive root.
Let M and N be the matrices
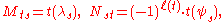
where ψs is given by the weight s−1ρ - λs. Then the matrix
is triangular with respect to any total order on W such that s ≥ t implies
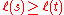.Steinberg proved that the entries of B are W-invariant exponential sums. Moreover its diagonal entries all equal 1, so it has determinant 1. Hence its inverse C has the same form. Define
If χ is an arbitrary exponential sum, then it follows that
with as the W-invariant exponential sum
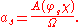
Indeed this is the unique solution of the system of equations