
Krein's condition
Encyclopedia
In mathematical analysis
, Krein's condition provides a necessary and sufficient condition for exponential sums

to be dense in a weighted L2 space on the real line. It was discovered by Mark Krein in the 1940s. A corollary, also called Krein's condition, provides a sufficient condition for the indeterminacy of the moment problem.
on the real line, dμ(x) = f(x) dx. The exponential sums
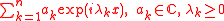
are dense in L2(μ) if and only if
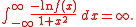

of μ are finite. If
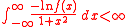
holds, then the Hamburger moment problem for μ is indeterminate; that is, there exists another measure ν ≠ μ on R such that

This can be derived from the "only if" part of Krein's theorem above.

the measure dμ(x) = f(x) dx is called the Stieltjes–Wigert measure. Since

the Hamburger moment problem for μ is indeterminate.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Krein's condition provides a necessary and sufficient condition for exponential sums

to be dense in a weighted L2 space on the real line. It was discovered by Mark Krein in the 1940s. A corollary, also called Krein's condition, provides a sufficient condition for the indeterminacy of the moment problem.
Statement
Let μ be an absolutely continuous measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the real line, dμ(x) = f(x) dx. The exponential sums
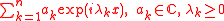
are dense in L2(μ) if and only if
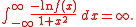
Indeterminacy of the moment problem
Let μ be as above; assume that all the momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...

of μ are finite. If
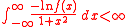
holds, then the Hamburger moment problem for μ is indeterminate; that is, there exists another measure ν ≠ μ on R such that

This can be derived from the "only if" part of Krein's theorem above.
Example
Let
the measure dμ(x) = f(x) dx is called the Stieltjes–Wigert measure. Since

the Hamburger moment problem for μ is indeterminate.

