Kruskal's algorithm
Encyclopedia
Kruskal's algorithm is an algorithm
in graph theory
that finds a minimum spanning tree
for a connected
weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex
, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component
). Kruskal's algorithm is an example of a greedy algorithm
.
This algorithm first appeared in Proceedings of the American Mathematical Society
, pp. 48–50 in 1956, and was written by Joseph Kruskal
.
Other algorithms for this problem include Prim's algorithm
, Reverse-Delete algorithm
, and Borůvka's algorithm
.
At the termination of the algorithm
, the forest has only one component and forms a minimum spanning tree of the graph
E) time, or equivalently, O(E log V) time, all with simple data structures. These running times are equivalent because:
We can achieve this bound as follows: first sort the edges by weight using a comparison sort
in O(E log E) time; this allows the step "remove an edge with minimum weight from S" to operate in constant time. Next, we use a disjoint-set data structure
(Union&Find) to keep track of which vertices are in which components. We need to perform O(E) operations, two 'find' operations and possibly one union for each edge. Even a simple disjoint-set data structure such as disjoint-set forests with union by rank can perform O(E) operations in O(E log V) time. Thus the total time is O(E log E) = O(E log V).
Provided that the edges are either already sorted or can be sorted in linear time (for example with counting sort
or radix sort
), the algorithm can use more sophisticated disjoint-set data structure
to run in O(E α(V)) time, where α is the extremely slowly-growing inverse of the single-valued Ackermann function
.
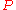be a connected, weighted graph and let 
be the subgraph of 
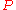produced by the algorithm. 
cannot have a cycle, since the last edge added to that cycle would have been within one subtree and not between two different trees. 
cannot be disconnected, since the first encountered edge that joins two components of 
would have been added by the algorithm. Thus, 
is a spanning tree of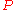 
.
: If F is the set of edges chosen at any stage of the algorithm, then there is some minimum spanning tree that contains F.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
that finds a minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
for a connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
). Kruskal's algorithm is an example of a greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
.
This algorithm first appeared in Proceedings of the American Mathematical Society
Proceedings of the American Mathematical Society
Proceedings of the American Mathematical Society is a monthly mathematics journal published by the American Mathematical Society. As a requirement, all articles must be at most 15 printed pages....
, pp. 48–50 in 1956, and was written by Joseph Kruskal
Joseph Kruskal
Joseph Bernard Kruskal, Jr. was an American mathematician, statistician, computer scientist and psychometrician. He was a student at the University of Chicago and at Princeton University, where he completed his Ph.D. in 1954, nominally under Albert W...
.
Other algorithms for this problem include Prim's algorithm
Prim's algorithm
In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
, Reverse-Delete algorithm
Reverse-delete algorithm
The reverse-delete algorithm is an algorithm in graph theory used to obtain a minimum spanning tree from a given connected, edge-weighed graph. If the graph is disconnected, this algorithm will find a minimum spanning tree for each disconnected part of the graph...
, and Borůvka's algorithm
Boruvka's algorithm
Borůvka's algorithm is an algorithm for finding a minimum spanning tree in a graph for which all edge weights are distinct.It was first published in 1926 by Otakar Borůvka as a method of constructing an efficient electricity network for Moravia....
.
Description
- create a forest F (a set of trees), where each vertex in the graph is a separate treeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
- create a set S containing all the edges in the graph
- while S is nonempty and F is not yet spanning
- remove an edge with minimum weight from S
- if that edge connects two different trees, then add it to the forest, combining two trees into a single tree
- otherwise discard that edge.
At the termination of the algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, the forest has only one component and forms a minimum spanning tree of the graph
Performance
Where E is the number of edges in the graph and V is the number of vertices, Kruskal's algorithm can be shown to run in O(E logBinary logarithm
In mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,...
E) time, or equivalently, O(E log V) time, all with simple data structures. These running times are equivalent because:
- E is at most V2 and
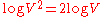
is O(log V). - If we ignore isolated vertices, which will each be their own component of the minimum spanning forest, V ≤ E+1, so log V is O(log E).
We can achieve this bound as follows: first sort the edges by weight using a comparison sort
Comparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
in O(E log E) time; this allows the step "remove an edge with minimum weight from S" to operate in constant time. Next, we use a disjoint-set data structure
Disjoint-set data structure
In computing, a disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of disjoint subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:* Find: Determine which set a particular element...
(Union&Find) to keep track of which vertices are in which components. We need to perform O(E) operations, two 'find' operations and possibly one union for each edge. Even a simple disjoint-set data structure such as disjoint-set forests with union by rank can perform O(E) operations in O(E log V) time. Thus the total time is O(E log E) = O(E log V).
Provided that the edges are either already sorted or can be sorted in linear time (for example with counting sort
Counting sort
In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that have each distinct key value, and using arithmetic on those counts to...
or radix sort
Radix sort
In computer science, radix sort is a non-comparative integer sorting algorithm that sorts data with integer keys by grouping keys by the individual digits which share the same significant position and value...
), the algorithm can use more sophisticated disjoint-set data structure
Disjoint-set data structure
In computing, a disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of disjoint subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:* Find: Determine which set a particular element...
to run in O(E α(V)) time, where α is the extremely slowly-growing inverse of the single-valued Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
.
Example
| Image | Description |
|---|---|
 |
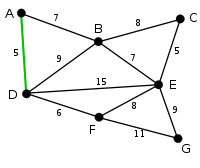AD and CE are the shortest arcs, with length 5, and AD has been arbitrarily Arbitrary Arbitrariness is a term given to choices and actions subject to individual will, judgment or preference, based solely upon an individual's opinion or discretion.Arbitrary decisions are not necessarily the same as random decisions... chosen, so it is highlighted. |
 |
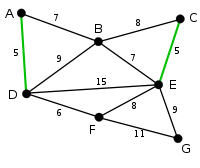CE is now the shortest arc that does not form a cycle, with length 5, so it is highlighted as the second arc. |
 |
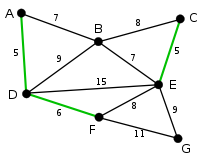The next arc, DF with length 6, is highlighted using much the same method. |
 |
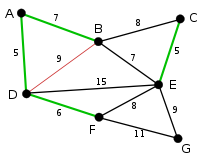The next-shortest arcs are AB and BE, both with length 7. AB is chosen arbitrarily, and is highlighted. The arc BD has been highlighted in red, because there already exists a path (in green) between B and D, so it would form a cycle (ABD) if it were chosen. |
 |
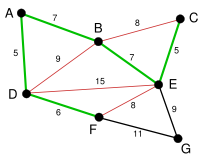The process continues to highlight the next-smallest arc, BE with length 7. Many more arcs are highlighted in red at this stage: BC because it would form the loop BCE, DE because it would form the loop DEBA, and FE because it would form FEBAD. |
 |
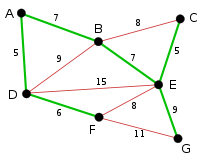Finally, the process finishes with the arc EG of length 9, and the minimum spanning tree is found. |
Proof of correctness
The proof consists of two parts. First, it is proved that the algorithm produces a spanning tree. Second, it is proved that the constructed spanning tree is of minimal weight.Spanning tree
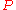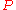Let be a connected, weighted graph and let be the subgraph of produced by the algorithm. cannot have a cycle, since the last edge added to that cycle would have been within one subtree and not between two different trees. cannot be disconnected, since the first encountered edge that joins two components of would have been added by the algorithm. Thus, is a spanning tree of 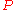.Minimality
We show that the following proposition P is true by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
: If F is the set of edges chosen at any stage of the algorithm, then there is some minimum spanning tree that contains F.
- Clearly P is true at the beginning, when F is empty: any minimum spanning tree will do, and there exists one because a weighted connected graph always has a minimum spanning tree.
- Now assume P is true for some non-final edge set F and let T be a minimum spanning tree that contains F. If the next chosen edge e is also in T, then P is true for F + e. Otherwise, T + e has a cycle C and there is another edge f that is in C but not F. (If there were no such edge f, then e could not have been added to F, since doing so would have created the cycle C.) Then T − f + e is a tree, and it has the same weight as T, since T has minimum weight and the weight of f cannot be less than the weight of e, otherwise the algorithm would have chosen f instead of e. So T − f + e is a minimum spanning tree containing F + e and again P holds.
- Therefore, by the principle of induction, P holds when F has become a spanning tree, which is only possible if F is a minimum spanning tree itself.