Krylov-Bogoliubov averaging method
Encyclopedia
The Krylov–Bogolyubov averaging method (Krylov–Bogolyubov method of averaging) is a mathematical method for approximate analysis of oscillating processes in non-linear mechanics. The method is based on the averaging principle when the exact differential equation of the motion is replaced by its averaged version. The method is named after Nikolay Krylov
and Nikolay Bogoliubov.
Various averaging schemes for studying problems of celestial mechanics were used since works of Gauss
, Fatou
, Delone, Hill
. The importance of the contribution of Krylov and Bogoliubov is that they developed a general averaging approach and proved that the solution of the averaged system approximates the exact dynamics.
problems of oscillatory type, for example Einstein's correction to the perihelion precession of Mercury .
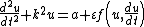
for a smooth function f along with appropriate initial conditions. The parameter ε is assumed to satisfy
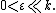
If ε = 0 then the equation becomes that of the simple harmonic oscillator with constant forcing, and the general solution is
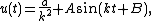
where A and B are chosen to match the initial conditions. The solution to the perturbed equation (when ε ≠ 0) is assumed to take the same
form, but now A and B are allowed to vary with t (and ε). If it is also assumed that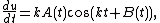
then it can be shown that A and B satisfy the differential equation: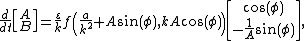
where
. Note that this equation is still exact — no approximation has been made as yet. The method of Krylov and Bogolyubov is to note that the functions A and B vary slowly
with time (in proportion to ε), so their dependence on φ can be (approximately) removed by averaging on the right hand side of the previous equation: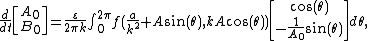
where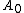
and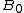 
are held fixed during the integration. After solving this (possibly) simpler set of differential equations, the Krylov–Bogolyubov averaged approximation for the original function is then given by
This approximation has been shown to satisfy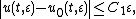
where t satisfies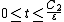
for some constants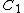
and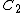 
, independent of ε.
Nikolay Mitrofanovich Krylov
Nikolay Mitrofanovich Krylov was a Russian and Soviet mathematician known for works on interpolation, non-linear mechanics, and numerical methods for solving equations of mathematical physics.-Biography:...
and Nikolay Bogoliubov.
Various averaging schemes for studying problems of celestial mechanics were used since works of Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, Fatou
Pierre Fatou
Pierre Joseph Louis Fatou was a French mathematician working in the field of complex analytic dynamics. He entered the École Normale Supérieure in Paris in 1898 to study mathematics and graduated in 1901 when he was appointed an astronomy post in the Paris Observatory...
, Delone, Hill
George William Hill
George William Hill , was an American astronomer and mathematician.Hill was born in New York City, New York to painter and engraver John William Hill. and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from...
. The importance of the contribution of Krylov and Bogoliubov is that they developed a general averaging approach and proved that the solution of the averaged system approximates the exact dynamics.
Background
Krylov-Bogoliubov averaging can be used to approximate oscillatory problems when a classical perturbation expansion fails. That is singular perturbationSingular perturbation
In mathematics, more precisely in perturbation theory, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero...
problems of oscillatory type, for example Einstein's correction to the perihelion precession of Mercury .
Derivation
The method deals differential equations in the form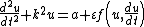for a smooth function f along with appropriate initial conditions. The parameter ε is assumed to satisfy
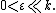
If ε = 0 then the equation becomes that of the simple harmonic oscillator with constant forcing, and the general solution is
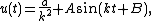
where A and B are chosen to match the initial conditions. The solution to the perturbed equation (when ε ≠ 0) is assumed to take the same
form, but now A and B are allowed to vary with t (and ε). If it is also assumed that
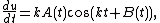
then it can be shown that A and B satisfy the differential equation:
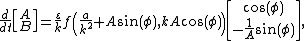
where
. Note that this equation is still exact — no approximation has been made as yet. The method of Krylov and Bogolyubov is to note that the functions A and B vary slowlywith time (in proportion to ε), so their dependence on φ can be (approximately) removed by averaging on the right hand side of the previous equation:
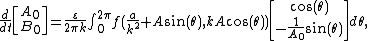
where
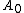and 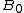are held fixed during the integration. After solving this (possibly) simpler set of differential equations, the Krylov–Bogolyubov averaged approximation for the original function is then given byThis approximation has been shown to satisfy
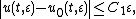
where t satisfies
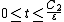
for some constants
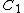and 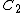, independent of ε.