Singular perturbation
Encyclopedia
In mathematics
, more precisely in perturbation theory
, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero. This is in contrast to regular perturbation
problems, for which an approximation can be obtained by simply setting the small parameter to zero.
More precisely, the solution cannot be uniformly approximated by an asymptotic expansion
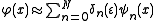
as
. Here 
is the small parameter of the problem and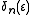 
are a sequence of functions of 
of increasing order, such as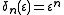 
. This is in contrast to regular perturbation
problems, for which a uniform approximation of this form can be obtained.
Singularly perturbed problems are generally characterized by dynamics operating on multiple scales. Several classes of singular perturbations are outlined below.
has a regular perturbation
. Most often in applications, an acceptable approximation to a regularly perturbed problem is found by simply replacing the small parameter
by zero everywhere in the problem statement. This corresponds to taking only the first term of the expansion, yielding an approximation that converges, perhaps slowly, to the true solution as 
decreases. The solution to a singularly perturbed problem cannot be approximated in this way: As seen in the examples below, a singular perturbation generally occurs when a problem's small parameter multiplies its highest operator. Thus naively taking the parameter to be zero changes the very nature of the problem. In the case of differential equations, boundary conditions cannot be satisfied; in algebraic equations, the possible number of solutions is decreased.
Singular perturbation theory is a rich and ongoing area of exploration for mathematicians, physicists, and other researchers. The methods used to tackle problems in this field are many. The more basic of these include the method of matched asymptotic expansions
and WKB approximation
for spatial problems, and in time, the Poincaré-Lindstedt method
, the method of multiple scales and periodic averaging.
For books on singular perturbation in ODE and PDE's, see for example Holmes, Introduction to Perturbation Methods, Hinch, Perturbation methods or Bender
and Orszag
, Advanced Mathematical Methods for Scientists and Engineers.
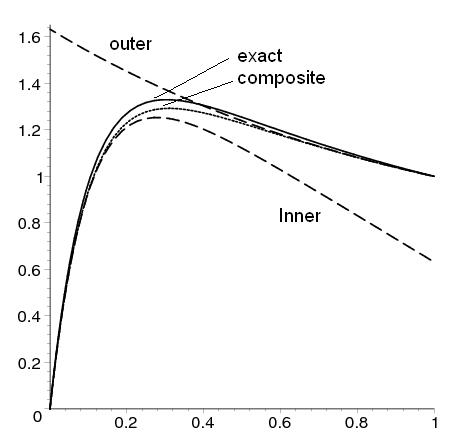
Differential equations that contain a small parameter that premultiplies the highest order term typically exhibit boundary layers, so that the solution evolves in two different scales. For example, consider the boundary value problem
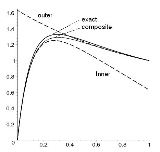
Its solution when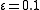
is the solid curve shown below. Note that the solution changes rapidly near the origin. If we naively set 
, we would get the solution labelled "outer" below which does not model the boundary layer, for which x is close to zero. For more details that show how to obtain the uniformly valid approximation, see method of matched asymptotic expansions
.
Consider a class of system described by following set of equations:
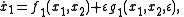
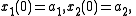
with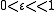
. The second equation indicates that the dynamics of 
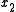is much faster than that of 
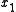. A theorem due to Tikhonov states that, with the correct conditions on the system, it will initially and very quickly approximate the solution to the equations
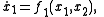
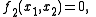
on some interval of time and that, as
decreases toward zero, the system will approach the solution more closely in that same interval.
, the properties of a slightly viscous fluid are dramatically different outside and inside a narrow boundary layer
. Thus the fluid exhibits multiple spatial scales.
Reaction-diffusion systems in which one reagent diffuses much more slowly than another can form spatial patterns
marked by areas where a reagent exists, and areas where it does not, with sharp transitions between them. In ecology
, predator-prey models such as
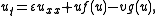
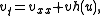
where
is the prey and 
is the predator, have been shown to exhibit such patterns.
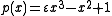. In the limit 
, this cubic
degenerates into the quadratic
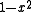with roots at 
.
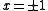Singular perturbation analysis suggests that the cubic has another root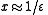
. Indeed, with 
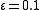, the roots are -0.955, 1.057, and 9.898. With 
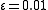, the roots are -0.995, 1.005, and 99.990. With 
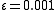, the roots are -0.9995, 1.0005, and 999.999.
In a sense, the problem has two different scales: two of the roots converge to finite numbers as
decreases, while the third becomes arbitrarily large.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero. This is in contrast to regular perturbation
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
problems, for which an approximation can be obtained by simply setting the small parameter to zero.
More precisely, the solution cannot be uniformly approximated by an asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
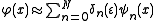
as
. Here is the small parameter of the problem and 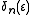are a sequence of functions of of increasing order, such as 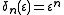. This is in contrast to regular perturbationPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
problems, for which a uniform approximation of this form can be obtained.
Singularly perturbed problems are generally characterized by dynamics operating on multiple scales. Several classes of singular perturbations are outlined below.
Methods of analysis
A perturbed problem whose solution can be approximated on the whole problem domain, whether space or time, by a single asymptotic expansionAsymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
has a regular perturbation
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. Most often in applications, an acceptable approximation to a regularly perturbed problem is found by simply replacing the small parameter
by zero everywhere in the problem statement. This corresponds to taking only the first term of the expansion, yielding an approximation that converges, perhaps slowly, to the true solution as decreases. The solution to a singularly perturbed problem cannot be approximated in this way: As seen in the examples below, a singular perturbation generally occurs when a problem's small parameter multiplies its highest operator. Thus naively taking the parameter to be zero changes the very nature of the problem. In the case of differential equations, boundary conditions cannot be satisfied; in algebraic equations, the possible number of solutions is decreased.Singular perturbation theory is a rich and ongoing area of exploration for mathematicians, physicists, and other researchers. The methods used to tackle problems in this field are many. The more basic of these include the method of matched asymptotic expansions
Method of matched asymptotic expansions
In mathematics, particularly in solving singularly perturbed differential equations, the method of matched asymptotic expansions is a common approach to finding an accurate approximation to a problem's solution.-Method overview:...
and WKB approximation
WKB approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
for spatial problems, and in time, the Poincaré-Lindstedt method
Poincaré-Lindstedt method
In perturbation theory, the Poincaré–Lindstedt method or Lindstedt–Poincaré method is a technique for uniformly approximating periodic solutions to ordinary differential equations, when regular perturbation approaches fail...
, the method of multiple scales and periodic averaging.
For books on singular perturbation in ODE and PDE's, see for example Holmes, Introduction to Perturbation Methods, Hinch, Perturbation methods or Bender
Carl M. Bender
Carl M. Bender is Wilfred R. and Ann Lee Konneker Distinguished Professor of Physics at Washington University in St. Louis.He received his A.B. in 1964 from Cornell University, where he graduated summa cum laude and with Distinction in All Subjects. He earned his M.A...
and Orszag
Steven A. Orszag
Steven Alan Orszag was an American mathematician. He was the Percey F. Smith Professor of Mathematics at Yale University from 2000 until his death in 2011, having joined the Yale faculty in 1998. Earlier, he was the Forrest E...
, Advanced Mathematical Methods for Scientists and Engineers.
Examples of singular perturbative problems
Each of the examples described below shows how a naive perturbation analysis, which assumes that the problem is regular instead of singular, will fail. Some show how the problem may be solved by more sophisticated singular methods.Vanishing coefficients in ordinary differential equations
Differential equations that contain a small parameter that premultiplies the highest order term typically exhibit boundary layers, so that the solution evolves in two different scales. For example, consider the boundary value problem
Its solution when
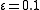is the solid curve shown below. Note that the solution changes rapidly near the origin. If we naively set , we would get the solution labelled "outer" below which does not model the boundary layer, for which x is close to zero. For more details that show how to obtain the uniformly valid approximation, see method of matched asymptotic expansionsMethod of matched asymptotic expansions
In mathematics, particularly in solving singularly perturbed differential equations, the method of matched asymptotic expansions is a common approach to finding an accurate approximation to a problem's solution.-Method overview:...
.
Examples in time
An electrically driven robot manipulator can have slower mechanical dynamics and faster electrical dynamics, thus exhibiting two time scales. In such cases, we can divide the system into two subsystems, one corresponding to faster dynamics and other corresponding to slower dynamics, and then design controllers for each one of them separately. Through a singular perturbation technique, we can make these two subsystems independent of each other, thereby simplifying the control problem.Consider a class of system described by following set of equations:
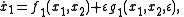
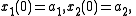
with
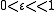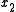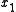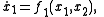
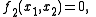
. The second equation indicates that the dynamics of is much faster than that of . A theorem due to Tikhonov states that, with the correct conditions on the system, it will initially and very quickly approximate the solution to the equationson some interval of time and that, as
decreases toward zero, the system will approach the solution more closely in that same interval.Examples in space
In fluid mechanicsFluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, the properties of a slightly viscous fluid are dramatically different outside and inside a narrow boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
. Thus the fluid exhibits multiple spatial scales.
Reaction-diffusion systems in which one reagent diffuses much more slowly than another can form spatial patterns
Pattern formation
The science of pattern formation deals with the visible, orderly outcomes of self-organisation and the common principles behind similar patterns....
marked by areas where a reagent exists, and areas where it does not, with sharp transitions between them. In ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
, predator-prey models such as
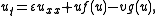
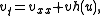
where
is the prey and is the predator, have been shown to exhibit such patterns.Algebraic equations
Consider the problem of finding all roots of the polynomial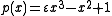. In the limit , this cubicCubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
degenerates into the quadratic
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
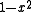with roots at 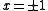.Singular perturbation analysis suggests that the cubic has another root
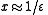. Indeed, with 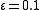, the roots are -0.955, 1.057, and 9.898. With 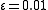, the roots are -0.995, 1.005, and 99.990. With 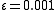, the roots are -0.9995, 1.0005, and 999.999.In a sense, the problem has two different scales: two of the roots converge to finite numbers as
decreases, while the third becomes arbitrarily large.