
Poincaré-Lindstedt method
Encyclopedia
In perturbation theory
, the Poincaré–Lindstedt method or Lindstedt–Poincaré method is a technique for uniformly approximating periodic
solutions to ordinary differential equation
s, when regular perturbation approaches fail. The method removes secular terms—terms growing without bound—arising in the straightforward application of perturbation theory
to weakly nonlinear problems with finite oscillatory solutions.
The method is named after Henri Poincaré
, and Anders Lindstedt
.

for t > 0, with 0 < ε 1.
Consider initial conditions
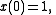
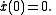
A perturbation-series
solution of the form x(t) = x0(t) + ε x1(t) + … is sought. The first two terms of the series are
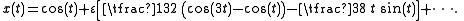
This approximation grows without bound in time, which is inconsistent with the physical system that the equation models. The term responsible for this unbounded growth, called the secular term, is t sin t. The Poincaré–Lindstedt method allows for the creation of an approximation that is accurate for all time, as follows.
In addition to expressing the solution itself as an asymptotic series, form another series with which to scale time t:
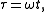 where
where 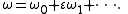
For convenience, take ω0 = 1 because the leading order of the solution's angular frequency
is 1. Then the original problem becomes
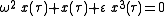
with the same initial conditions. Now search for a solution of the form x(τ) = x0(τ) + ε x1(τ) + … . The following solutions for the zeroth and first order problem in ε are obtained:
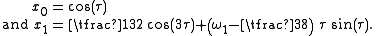
So the secular term can be removed through the choice: ω1 = . Higher orders of accuracy can be obtained by continuing the perturbation analysis along this way. As of now, the approximation—correct up to first order in ε—is

Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, the Poincaré–Lindstedt method or Lindstedt–Poincaré method is a technique for uniformly approximating periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
solutions to ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, when regular perturbation approaches fail. The method removes secular terms—terms growing without bound—arising in the straightforward application of perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
to weakly nonlinear problems with finite oscillatory solutions.
The method is named after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, and Anders Lindstedt
Anders Lindstedt
Anders Lindstedt was a Swedish mathematician, astronomer, and actuarial scientist, known for the Lindstedt-Poincaré method.- Life and work :...
.
Example: the Duffing equation
The undamped, unforced Duffing equation is given by
for t > 0, with 0 < ε 1.
Consider initial conditions
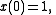
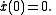
A perturbation-series
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
solution of the form x(t) = x0(t) + ε x1(t) + … is sought. The first two terms of the series are
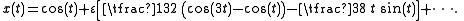
This approximation grows without bound in time, which is inconsistent with the physical system that the equation models. The term responsible for this unbounded growth, called the secular term, is t sin t. The Poincaré–Lindstedt method allows for the creation of an approximation that is accurate for all time, as follows.
In addition to expressing the solution itself as an asymptotic series, form another series with which to scale time t:
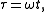 where
where 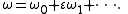
For convenience, take ω0 = 1 because the leading order of the solution's angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
is 1. Then the original problem becomes
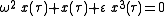
with the same initial conditions. Now search for a solution of the form x(τ) = x0(τ) + ε x1(τ) + … . The following solutions for the zeroth and first order problem in ε are obtained:
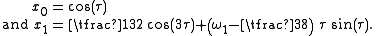
So the secular term can be removed through the choice: ω1 = . Higher orders of accuracy can be obtained by continuing the perturbation analysis along this way. As of now, the approximation—correct up to first order in ε—is


