Duffing equation
Encyclopedia
The Duffing equation is a non-linear second-order differential equation
used to model certain damped
and driven oscillators. The equation is given by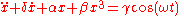
where the (unknown) function x=x(t) is the displacement at time t,
is the first derivative
of x with respect to time, i.e. velocity
, and
is the second time-derivative of x, i.e. acceleration
. The numbers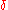
, 
, 
, 
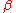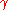and 
are given constants.
The equation describes the motion of a damped oscillator with a more complicated potential
than in simple harmonic motion
(which corresponds to the case β=δ=0); in physical terms, it models, for example, a spring pendulum
whose spring's stiffness
does not exactly obey Hooke's law
.
The Duffing equation is an example of a dynamical system that exhibits chaotic behavior
.
Moreover the Duffing system presents in the frequency response the jump resonance phenomenon that is a sort of frequency hysteresis behaviour.
In the special case of the undamped (
) and undrived (
) Duffing equation, an exact solution can be obtained using Jacobi's elliptic functions
.
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
used to model certain damped
Damping
In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
and driven oscillators. The equation is given by
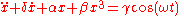
where the (unknown) function x=x(t) is the displacement at time t,
is the first derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of x with respect to time, i.e. velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, and
is the second time-derivative of x, i.e. accelerationAcceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
. The numbers
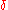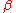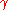, , , and are given constants.The equation describes the motion of a damped oscillator with a more complicated potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
than in simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
(which corresponds to the case β=δ=0); in physical terms, it models, for example, a spring pendulum
Spring pendulum
A spring pendulum is a physical system where a mass is connected to a spring so that the resulting motion contains elements of a simple pendulum as well as a spring. The system is much more complex than a simple pendulum because the properties of the spring adds an extra dimension of freedom to...
whose spring's stiffness
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
does not exactly obey Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
.
The Duffing equation is an example of a dynamical system that exhibits chaotic behavior
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
.
Moreover the Duffing system presents in the frequency response the jump resonance phenomenon that is a sort of frequency hysteresis behaviour.
Parameters
-
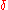controls the size of the damping (friction). -
controls the size of the restoring force. -
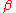controls the amount of non-linearity in the restoring force. If 
, the Duffing equation describes a damped and driven simple harmonic oscillator. -
controls the amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the periodic driving force. If
we have a system without driving force. -
controls the frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
of the periodic driving force.
Methods of solution
In general, the Duffing equation does not admit an exact symbolic solution. However, many approximate methods work well:- Expansion in a Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
will provide an equation of motion to arbitrary precision. - The
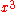term, also called the Duffing term, can be approximated as small and the system treated as a perturbedPerturbation theoryPerturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
simple harmonic oscillator. - The Frobenius methodFrobenius methodIn mathematics, the Frobenius method, named after Ferdinand Georg Frobenius, is a way to find an infinite series solution for a second-order ordinary differential equation of the formin the vicinity of the regular singular point z=0....
yields a complicated but workable solution. - Any of the various numeric methodsNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
such as Euler's method and Runge-Kutta can be used.
In the special case of the undamped (
) and undrived () Duffing equation, an exact solution can be obtained using Jacobi's elliptic functionsJacobi's elliptic functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...
.