Lagrange's four-square theorem
Encyclopedia
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number
can be represented as the sum of four integer squares
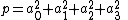
where the four numbers are integers. For illustration, 3, 31 and 310 can be represented as the sum of four squares as follows:
This theorem was proven by Joseph Louis Lagrange
in 1770, and corresponds to Fermat's theorem on sums of two squares.
of Diophantus
, translated into Latin by Bachet
in 1621.
Adrien-Marie Legendre
improved on the theorem in 1798 by stating that a positive integer can be expressed as the sum of three squares if and only if
it is not of the form . His proof was incomplete, leaving a gap which was later filled by Carl Friedrich Gauss
.
s, which are the analog of integer
s for quaternion
s. The Hurwitz quaternions consist of all quaternions with integer components and all quaternions with half-integer components. These two sets can be combined into a single formula
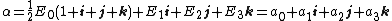
where are integers. Thus, the quaternion components are either all integers or all half-integers, depending on whether is even or odd, respectively. The set of Hurwitz quaternions forms a ring
; in particular, the sum or product of any two Hurwitz quaternions is likewise a Hurwitz quaternion.
The generalized Euclidean algorithm identifies the greatest common right or left divisor of two Hurwitz quaternions, where the "size" of the remainder is measured by the norm. The norm
of a quaternion is the nonnegative real number
,
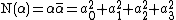where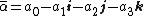
is the conjugate of .
Since quaternion multiplication is associative, and real numbers commute with other quaternions, the norm of a product of quaternions equals the product of the norms:
.
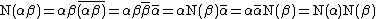Since any natural number can be factored into powers of primes, the four-square theorem holds for all natural numbers if it is true for all prime numbers. It is true for . To show this for an odd prime integer , represent it as a quaternion and assume that it can be factored into two Hurwitz quaternions
The norms of are nonnegative integers such that
But the norm has only two factors, both . Therefore, if it can be factored into Hurwitz quaternions, then is the sum of four squares
Lagrange
proved that any odd prime divides at least one number of the form , where and are integers. The latter number can be factored in Hurwitz quaternions:
If could not be factored in Hurwitz quaternions, it would be a Hurwitz prime number by definition. Then, by unique factorization, would have to divide either or to form another Hurwitz quaternion. But for , the number
is not a Hurwitz integer. Therefore, every can be factored in Hurwitz quaternions, and the four-square theorem holds.
and Waring's problem
. Another possible generalisation is the following problem: Given natural number
s , can we solve
for all positive integers in integers ? The case is answered in the positive by Lagrange's four-square theorem. The general solution was given by Ramanujan. He proved that if we assume, without loss of generality, that then there are exactly 54 possible choices for such that the problem is solvable in integers for all . (Ramanujan listed a 55th possibility , but in this case the problem is not solvable if . )
and Jeffrey Shallit
have found randomized
polynomial-time algorithms for computing a representation for a given integer , in expected running time .
These integers consist of the seven odd numbers 1, 3, 5, 7, 11, 15, 23 and all numbers of the form or .
The sequence of positive integers which cannot be represented as a sum of four non-zero squares is:
These integers consist of the eight odd numbers 1, 3, 5, 9, 11, 17, 29, 41 and all numbers of the form or .
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
can be represented as the sum of four integer squares
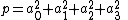
where the four numbers are integers. For illustration, 3, 31 and 310 can be represented as the sum of four squares as follows:
- .
This theorem was proven by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in 1770, and corresponds to Fermat's theorem on sums of two squares.
Historical development
The theorem appears in the ArithmeticaArithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
of Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
, translated into Latin by Bachet
Claude Gaspard Bachet de Méziriac
Claude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse.Bachet was a pupil of the Jesuit mathematician Jacques de Billy at the Jesuit College in Rheims...
in 1621.
Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
improved on the theorem in 1798 by stating that a positive integer can be expressed as the sum of three squares if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is not of the form . His proof was incomplete, leaving a gap which was later filled by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
.
Proof using the Hurwitz integers
One of the ways to prove the theorem relies on Hurwitz quaternionHurwitz quaternion
In mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
s, which are the analog of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s for quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s. The Hurwitz quaternions consist of all quaternions with integer components and all quaternions with half-integer components. These two sets can be combined into a single formula
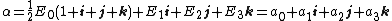
where are integers. Thus, the quaternion components are either all integers or all half-integers, depending on whether is even or odd, respectively. The set of Hurwitz quaternions forms a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
; in particular, the sum or product of any two Hurwitz quaternions is likewise a Hurwitz quaternion.
The generalized Euclidean algorithm identifies the greatest common right or left divisor of two Hurwitz quaternions, where the "size" of the remainder is measured by the norm. The norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of a quaternion is the nonnegative real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
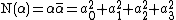,where
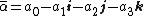is the conjugate of .Since quaternion multiplication is associative, and real numbers commute with other quaternions, the norm of a product of quaternions equals the product of the norms:
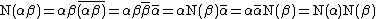.Since any natural number can be factored into powers of primes, the four-square theorem holds for all natural numbers if it is true for all prime numbers. It is true for . To show this for an odd prime integer , represent it as a quaternion and assume that it can be factored into two Hurwitz quaternions
- .
The norms of are nonnegative integers such that
- .
But the norm has only two factors, both . Therefore, if it can be factored into Hurwitz quaternions, then is the sum of four squares
- .
Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
proved that any odd prime divides at least one number of the form , where and are integers. The latter number can be factored in Hurwitz quaternions:
- .
If could not be factored in Hurwitz quaternions, it would be a Hurwitz prime number by definition. Then, by unique factorization, would have to divide either or to form another Hurwitz quaternion. But for , the number
is not a Hurwitz integer. Therefore, every can be factored in Hurwitz quaternions, and the four-square theorem holds.
Generalizations
Lagrange's four-square theorem is a special case of the Fermat polygonal number theoremFermat polygonal number theorem
In additive number theory, the Fermat polygonal number theorem states that every positive integer is a sum of at most -gonal numbers. That is, every positive number can be written as the sum of three or fewer triangular numbers, and as the sum of four or fewer square numbers, and as the sum of...
and Waring's problem
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
. Another possible generalisation is the following problem: Given natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s , can we solve
for all positive integers in integers ? The case is answered in the positive by Lagrange's four-square theorem. The general solution was given by Ramanujan. He proved that if we assume, without loss of generality, that then there are exactly 54 possible choices for such that the problem is solvable in integers for all . (Ramanujan listed a 55th possibility , but in this case the problem is not solvable if . )
Algorithms
Michael O. RabinMichael O. Rabin
Michael Oser Rabin , is an Israeli computer scientist and a recipient of the Turing Award.- Biography :Rabin was born in 1931 in Breslau, Germany, , the son of a rabbi. In 1935, he emigrated with his family to Mandate Palestine...
and Jeffrey Shallit
Jeffrey Shallit
Jeffrey Outlaw Shallit is a computer scientist, number theorist, a noted advocate for civil liberties on the Internet, and a noted critic of intelligent design. He is married to Anna Lubiw, also a computer scientist....
have found randomized
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
polynomial-time algorithms for computing a representation for a given integer , in expected running time .
Uniqueness
The sequence of positive integers whose representation as a sum of four squares is unique (up to order) is:- 1, 2, 3, 5, 6, 7, 8, 11, 14, 15, 23, 24, 32, 56, 96, 128, 224, 384, 512, 896 ... .
These integers consist of the seven odd numbers 1, 3, 5, 7, 11, 15, 23 and all numbers of the form or .
The sequence of positive integers which cannot be represented as a sum of four non-zero squares is:
- 1, 2, 3, 5, 6, 8, 9, 11, 14, 17, 24, 29, 32, 41, 56, 96, 128, 224, 384, 512, 896 ... .
These integers consist of the eight odd numbers 1, 3, 5, 9, 11, 17, 29, 41 and all numbers of the form or .
See also
- Euler's four-square identityEuler's four-square identityIn mathematics, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:=\,...
- 15 and 290 theorems
- Jacobi's four-square theoremJacobi's four-square theoremIn 1834, Carl Gustav Jakob Jacobi found an exact formula for the total number of ways a given positive integer n can be represented as the sum of four squares...