
Lagrange inversion theorem
Encyclopedia
In mathematical analysis
, the Lagrange inversion theorem, also known as the Lagrange-Bürmann formula, gives the Taylor series
expansion of the inverse function
of an analytic function
.
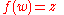
where f is analytic at a point a and f '(a) ≠ 0. Then it is possible to invert or solve the equation for w:
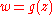
where g is analytic at the point b = f(a). This is also called reversion of series.
The series expansion of g is given by
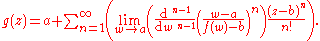
The formula is also valid for formal power series
and can be generalized in various ways. It can be formulated for functions of several variables, it can be extended to provide a ready formula for F(g(z)) for any analytic function F, and it can be generalized to the case f '(a) = 0, where the inverse g is a multivalued function.
The theorem was proved by Lagrange
and generalized by Hans Heinrich Bürmann
, both in the late 18th century. There is a straightforward derivation using complex analysis
and contour integration; the complex formal power series version is clearly a consequence of knowing the formula for polynomial
s, so the theory of analytic function
s may be applied. Actually, the machinery from analytic function theory enters only in a formal way in this proof, in that what is really needed is just some property of the formal residue, and a more direct formal proof is available.
and applies when and
and 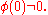 Take
Take  to obtain
to obtain  We have
We have
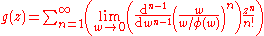

which can be written alternatively as
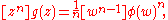
where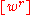 is an operator which extracts the coefficient of
is an operator which extracts the coefficient of  in what follows it.
in what follows it.
A useful generalization of the formula is known as the Lagrange–Bürmann formula: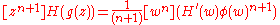
where can be an arbitrary analytic function, e.g. .
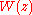 that is implicitly defined by the equation
that is implicitly defined by the equation
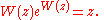
We may use the theorem to compute the Taylor series
of at
at 
We take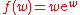 and
and 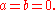 Recognizing that
Recognizing that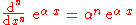
this gives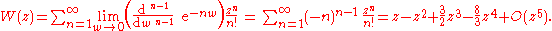
The radius of convergence
of this series is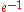 (this example refers to the principal branch
(this example refers to the principal branch
of the Lambert function).
A series that converges for larger z (though not for all z) can also be derived by series inversion. The function satisfies the equation
satisfies the equation
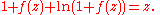
Then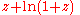 can be expanded into a power series and inverted. This gives a series for
can be expanded into a power series and inverted. This gives a series for  :
:
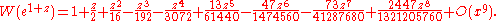
 can be computed by substituting
can be computed by substituting  for z in the above series. For example, substituting -1 for z gives the value of
for z in the above series. For example, substituting -1 for z gives the value of 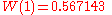 .
.
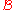 of unlabelled binary tree
of unlabelled binary tree
s.
An element of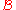 is either a leaf of size zero, or a root node with two subtrees. Denote by
is either a leaf of size zero, or a root node with two subtrees. Denote by  the number of binary trees on n nodes.
the number of binary trees on n nodes.
Note that removing the root splits a binary tree into two trees of smaller size. This yields the functional equation on the generating function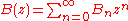 :
:
Now let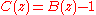 and rewrite this equation as follows:
and rewrite this equation as follows: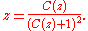
Now apply the theorem with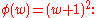
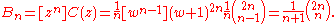
We conclude that is the Catalan number
is the Catalan number
.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the Lagrange inversion theorem, also known as the Lagrange-Bürmann formula, gives the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion of the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
.
Theorem statement
Suppose the dependence between the variables w and z is implicitly defined by an equation of the form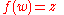
where f is analytic at a point a and f '(a) ≠ 0. Then it is possible to invert or solve the equation for w:
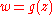
where g is analytic at the point b = f(a). This is also called reversion of series.
The series expansion of g is given by
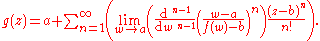
The formula is also valid for formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
and can be generalized in various ways. It can be formulated for functions of several variables, it can be extended to provide a ready formula for F(g(z)) for any analytic function F, and it can be generalized to the case f '(a) = 0, where the inverse g is a multivalued function.
The theorem was proved by Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
and generalized by Hans Heinrich Bürmann
Hans Heinrich Bürmann
Hans Heinrich Bürmann was a German mathematician and teacher. He ran an "academy of commerce" in Mannheim since 1795 where he used to teach mathematics. He also served as a censor in Mannheim. He was nominated Headmaster of the Commerce Academy of the Grand Duchy of Baden in 1811...
, both in the late 18th century. There is a straightforward derivation using complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
and contour integration; the complex formal power series version is clearly a consequence of knowing the formula for polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, so the theory of analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s may be applied. Actually, the machinery from analytic function theory enters only in a formal way in this proof, in that what is really needed is just some property of the formal residue, and a more direct formal proof is available.
Lagrange–Bürmann formula
There is a special case of Lagrange inversion theorem that is used in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and applies when
 and
and 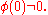 Take
Take  to obtain
to obtain  We have
We have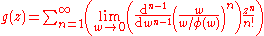

which can be written alternatively as
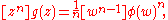
where
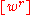 is an operator which extracts the coefficient of
is an operator which extracts the coefficient of  in what follows it.
in what follows it.A useful generalization of the formula is known as the Lagrange–Bürmann formula:
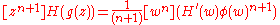
where can be an arbitrary analytic function, e.g. .
Lambert W function
The Lambert W function is the function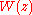 that is implicitly defined by the equation
that is implicitly defined by the equation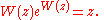
We may use the theorem to compute the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of
 at
at 
We take
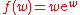 and
and 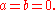 Recognizing that
Recognizing that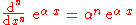
this gives
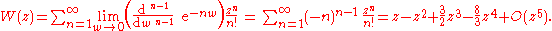
The radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of this series is
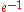 (this example refers to the principal branch
(this example refers to the principal branchPrincipal branch
In mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....
of the Lambert function).
A series that converges for larger z (though not for all z) can also be derived by series inversion. The function
 satisfies the equation
satisfies the equation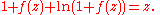
Then
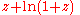 can be expanded into a power series and inverted. This gives a series for
can be expanded into a power series and inverted. This gives a series for  :
: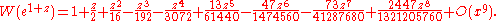
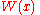 can be computed by substituting
can be computed by substituting 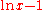 for z in the above series. For example, substituting -1 for z gives the value of
for z in the above series. For example, substituting -1 for z gives the value of 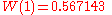 .
.Binary trees
Consider the set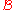 of unlabelled binary tree
of unlabelled binary treeBinary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
s.
An element of
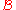 is either a leaf of size zero, or a root node with two subtrees. Denote by
is either a leaf of size zero, or a root node with two subtrees. Denote by  the number of binary trees on n nodes.
the number of binary trees on n nodes.Note that removing the root splits a binary tree into two trees of smaller size. This yields the functional equation on the generating function
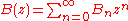 :
:
Now let
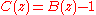 and rewrite this equation as follows:
and rewrite this equation as follows: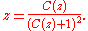
Now apply the theorem with
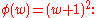
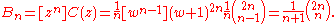
We conclude that
 is the Catalan number
is the Catalan numberCatalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
.
See also
- Faà di Bruno's formulaFaà di Bruno's formulaFaà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
gives coefficients of the composition of two formal power series in terms of the coefficients of those two series. Equivalently, it is a formula for the nth derivative of a composite function. - Lagrange reversion theoremLagrange reversion theoremIn mathematics, the Lagrange reversion theorem gives series or formal power series expansions of certain implicitly defined functions; indeed, of compositions with such functions....
for another theorem sometimes called the inversion theorem

