Lambek-Moser theorem
Encyclopedia
In combinatorial number theory, the Lambek–Moser theorem is a generalization of Beatty's theorem that defines a partition
of the positive integer
s into two subsets from any monotonic integer-valued function. Conversely, any partition of the positive integers into two subsets may be defined from a monotonic function in this way.
The theorem was discovered by Leo Moser
and Joachim Lambek
. provides a visual proof
of the result.
and unbounded function
ƒ that maps positive integers to non-negative integers. From any such function ƒ, define ƒ* to be the integer-valued function that is as close as possible to the inverse function
of ƒ, in the sense that, for all n,
Further, define
Then the result states that F and G are strictly increasing and that the ranges of F and G form a partition of the positive integers.
.
Thus F(n) = n2 + n and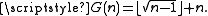
For n = 1, 2, 3, ... the values of F are the pronic number
s
while the values of G are
These two sequences are complementary: each positive integer belongs to exactly one of them. The Lambek–Moser theorem states that this phenomenon is not specific to the pronic numbers, but rather it arises for any choice of ƒ with the appropriate properties.
r > 1, can be seen as an instance of the Lambek–Moser theorem. In Beatty's theorem,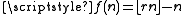
and 
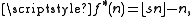where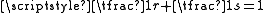 
. The condition that r (and therefore s) be greater than one implies that these two functions are non-decreasing; the derived functions are 
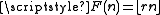and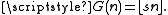 
The sequences of values of F and G forming the derived partition are known as Beatty sequences.
For instance, consider the partition of integers into even and odd numbers: let S be the even numbers and T be the odd numbers.
Then sn = 2n, so ƒ(n) = n and similarly ƒ*(n) = n − 1. These two functions ƒ and ƒ* form an inverse pair, and the partition generated via the Lambek–Moser theorem from this pair is just the partition of the positive integers into even and odd numbers.
Lambek and Moser discuss formulas involving the prime-counting function for the functions ƒ and ƒ* arising in this way from the partition of the positive integers into prime number
s and composite number
s.
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of the positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s into two subsets from any monotonic integer-valued function. Conversely, any partition of the positive integers into two subsets may be defined from a monotonic function in this way.
The theorem was discovered by Leo Moser
Leo Moser
Leo Moser was an Austrian-Canadian mathematician, best known for his polygon notation....
and Joachim Lambek
Joachim Lambek
Joachim Lambek is Peter Redpath Emeritus Professor of Pure Mathematics at McGill University, where he earned his Ph.D. degree in 1950 with Hans Julius Zassenhaus as advisor. He is called Jim by his friends.- Scholarly work :...
. provides a visual proof
Proof without words
In mathematics, a proof without words is a proof of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than more formal and mathematically rigorous proofs due to their...
of the result.
Statement of the theorem
The theorem applies to any non-decreasingMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
and unbounded function
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
ƒ that maps positive integers to non-negative integers. From any such function ƒ, define ƒ* to be the integer-valued function that is as close as possible to the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of ƒ, in the sense that, for all n,
- ƒ(ƒ*(n)) < n ≤ ƒ(ƒ*(n) + 1). It follows from this definition that ƒ** = ƒ.
Further, define
- F(n) = ƒ(n) + n and G(n) = ƒ*(n) + n.
Then the result states that F and G are strictly increasing and that the ranges of F and G form a partition of the positive integers.
Example
Let ƒ(n) = n2; then.Thus F(n) = n2 + n and
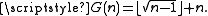
For n = 1, 2, 3, ... the values of F are the pronic number
Pronic number
A pronic number, oblong number, rectangular number or heteromecic number, is a number which is the product of two consecutive integers, that is, n . The n-th pronic number is twice the n-th triangular number and n more than the n-th square number...
s
- 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, ...
while the values of G are
- 1, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, ....
These two sequences are complementary: each positive integer belongs to exactly one of them. The Lambek–Moser theorem states that this phenomenon is not specific to the pronic numbers, but rather it arises for any choice of ƒ with the appropriate properties.
Beatty's theorem
Beatty's theorem, defining a partition of the integers from rounding their multiples by an irrational numberIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
r > 1, can be seen as an instance of the Lambek–Moser theorem. In Beatty's theorem,
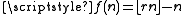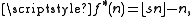and where 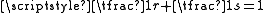. The condition that r (and therefore s) be greater than one implies that these two functions are non-decreasing; the derived functions are 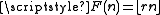and 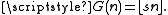The sequences of values of F and G forming the derived partition are known as Beatty sequences.Universality
The Lambek–Moser theorem is universal, in the sense that it can explain any partition of the integers into two infinite parts. If S = s1,s2,... and T = t1,t2,... are any two infinite subsets forming a partition of the integers, one may construct a pair of functions ƒ and ƒ* from which this partition may be derived using the Lambek–Moser theorem: define ƒ(n) = sn − n and ƒ*(n) = tn − n.For instance, consider the partition of integers into even and odd numbers: let S be the even numbers and T be the odd numbers.
Then sn = 2n, so ƒ(n) = n and similarly ƒ*(n) = n − 1. These two functions ƒ and ƒ* form an inverse pair, and the partition generated via the Lambek–Moser theorem from this pair is just the partition of the positive integers into even and odd numbers.
Lambek and Moser discuss formulas involving the prime-counting function for the functions ƒ and ƒ* arising in this way from the partition of the positive integers into prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s and composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
s.