Lamplighter group
Encyclopedia
In mathematics
, the lamplighter group L of group theory
is the wreath product
Z/2Z ≀ Z. The base group
B of L is
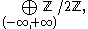
and so L/B is isomorphic to Z.
The standard presentation
for the lamplighter group arises from the wreath product structure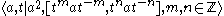
, which may be simplified to
.
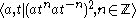The generators a and t are intrinsic to the group's notable growth rate
, though they are sometimes replaced with a and at, changing the logarithm of the growth rate by at most a factor of 2.
The name of the group comes from viewing the group as acting on a doubly infinite sequence of street lamps ..., l-2, l-1, l0, l1, l2, ... , each of which may be on or off, and a lamplighter
standing at some lamp lk. The generator t increments k, so that the lamplighter moves to the next lamp (t -1 decrements k), while the generator a means that the state of lamp lk is changed (from off to on or from on to off).
We may assume that only finitely many lamps are lit at any time, since the action of any element of L changes at most finitely many lamps. The number of lamps lit is, however, unbounded. The group action is thus similar to the action of a Turing machine
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the lamplighter group L of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
is the wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
Z/2Z ≀ Z. The base group
Base (group theory)
Let G be a finite permutation group acting on a set \Omega. A sequenceB = [\beta_1,\beta_2,...,\beta_k]of k distinct elements of \Omega is a base for G if the only element of G which fixes every \beta_i \in B pointwise is the identity element of G....
B of L is
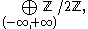
and so L/B is isomorphic to Z.
The standard presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
for the lamplighter group arises from the wreath product structure
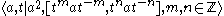, which may be simplified to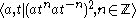.The generators a and t are intrinsic to the group's notable growth rate
Growth rate (group theory)
In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
, though they are sometimes replaced with a and at, changing the logarithm of the growth rate by at most a factor of 2.
The name of the group comes from viewing the group as acting on a doubly infinite sequence of street lamps ..., l-2, l-1, l0, l1, l2, ... , each of which may be on or off, and a lamplighter
Lamplighter
A lamplighter, historically, was an employee of a town who lit street lights, generally by means of a wick on a long pole. At dawn, they would return and extinguish them using a small hook on the same pole. Early street lights were generally candles, oil, and similar consumable liquid or solid...
standing at some lamp lk. The generator t increments k, so that the lamplighter moves to the next lamp (t -1 decrements k), while the generator a means that the state of lamp lk is changed (from off to on or from on to off).
We may assume that only finitely many lamps are lit at any time, since the action of any element of L changes at most finitely many lamps. The number of lamps lit is, however, unbounded. The group action is thus similar to the action of a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
.