
Large set (Ramsey theory)
Encyclopedia
In Ramsey theory
, a set S of natural number
s is considered to be a large set if and only if Van der Waerden's theorem can be generalized to assert the existence of arithmetic progressions with common difference in S. That is, S is large if and only if every finite partition of the natural numbers has a cell containing arbitrarily long arithmetic progressions having common differences in S.
Two sufficient conditions are:
The first sufficient condition implies that if S is a thick set, then S is large.
Other facts about large sets include:
If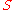 is large, then for any
is large, then for any  ,
, 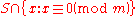 is large.
is large.
It is unknown whether there are 2-large sets that are not also large sets. Brown, Graham, and Landman (1999) conjecture that no such set exists.
Ramsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
, a set S of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is considered to be a large set if and only if Van der Waerden's theorem can be generalized to assert the existence of arithmetic progressions with common difference in S. That is, S is large if and only if every finite partition of the natural numbers has a cell containing arbitrarily long arithmetic progressions having common differences in S.
Examples
- The natural numbers are large. This is precisely the assertion of Van der Waerden's theorem.
- The even numbers are large.
Properties
Necessary conditions for largeness include:- If S is large, for any natural number n, S must contain infinitely many multiples of n.
- If
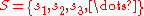 is large, it is not the case that sk≥3sk-1 for k≥ 2.
is large, it is not the case that sk≥3sk-1 for k≥ 2.
Two sufficient conditions are:
- If S contains n-cubes for arbitrarily largeArbitrarily largeIn mathematics, the phrase arbitrarily large, arbitrarily small, arbitrarily long is used in statements such as:which is shorthand for:This should not be confused with the phrase "sufficiently large"...
n, then S is large. - If
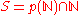 where
where 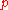 is a polynomial with
is a polynomial with  and positive leading coefficient, then
and positive leading coefficient, then  is large.
is large.
The first sufficient condition implies that if S is a thick set, then S is large.
Other facts about large sets include:
- If S is large and F is finite, then S –Complement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
F is large. 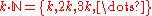 is large. Similarly, if S is large,
is large. Similarly, if S is large,  is also large.
is also large.
If
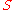 is large, then for any
is large, then for any  ,
, 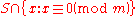 is large.
is large.2-large and k-large sets
A set is k-large, for a natural number k > 0, when it meets the conditions for largeness when the restatement of van der Waerden's theorem is concerned only with k-colorings. Every set is either large or k-large for some maximal k. This follows from two important, albeit trivially true, facts:- k-largeness implies (k-1)-largeness for k>1
- k-largeness for all k implies largeness.
It is unknown whether there are 2-large sets that are not also large sets. Brown, Graham, and Landman (1999) conjecture that no such set exists.

