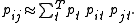Latent class model
Encyclopedia
In statistics
, a latent class model (LCM) relates a set of observed discrete multivariate variables to a set of latent variable
s. It is a type of latent variable model
. It is called a latent class model because the latent variable is discrete. A class is characterized by a pattern of conditional probabilities that indicate the chance that variables take on certain values.
Latent Class Analysis (LCA) is a subset of structural equation modeling
, used to find groups or subtypes of cases in multivariate categorical data. These subtypes are called "latent classes".
Confronted with a situation as follows, a researcher might choose to use LCA to understand the data: Imagine that symptoms a-d have been measured in a range of patients with diseases X Y and Z, and that disease X is associated with the presence of symptoms a, b, and c, disease Y with symptoms b, c, d, and disease Z with symptoms a, c and d.
The LCA will attempt to detect the presence of latent classes (the disease entities), creating patterns of association in the symptoms. As in factor analysis, the LCA can also be used to classify case according to their maximum likelihood
class membership.
Because the criterion for solving the LCA is to achieve latent classes within which there is no longer any association of one symptom with another (because the class is the disease which causes their association, and the set of diseases a patient has (or class a case is a member of) causes the symptom association, the symptoms will be "conditionally independent", i.e., conditional on class membership, they are no longer related.
As a practical instance, the variables could be multiple choice
items of a political questionnaire. The data in this case consists of a N-way contingency table
with answers to the items for a number of respondents. In this example, the latent variable refers to political opinion and the latent classes to political groups. Given group membership, the conditional probabilities specify the chance certain answers are chosen.
Within each latent class, the observed variables are statistically independent. This is an important aspect. Usually the observed variables are statistically dependent. By introducing the latent variable, independence is restored in the sense that within classes variables are independent (local independence
). We then say that the association between the observed variables is explained by the classes of the latent variable (McCutcheon, 1987).
In one form the latent class model is written as
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a latent class model (LCM) relates a set of observed discrete multivariate variables to a set of latent variable
Latent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
s. It is a type of latent variable model
Latent variable model
A latent variable model is a statistical model that relates a set of variables to a set of latent variables.It is assumed that 1) the responses on the indicators or manifest variables are the result of...
. It is called a latent class model because the latent variable is discrete. A class is characterized by a pattern of conditional probabilities that indicate the chance that variables take on certain values.
Latent Class Analysis (LCA) is a subset of structural equation modeling
Structural equation modeling
Structural equation modeling is a statistical technique for testing and estimating causal relations using a combination of statistical data and qualitative causal assumptions...
, used to find groups or subtypes of cases in multivariate categorical data. These subtypes are called "latent classes".
Confronted with a situation as follows, a researcher might choose to use LCA to understand the data: Imagine that symptoms a-d have been measured in a range of patients with diseases X Y and Z, and that disease X is associated with the presence of symptoms a, b, and c, disease Y with symptoms b, c, d, and disease Z with symptoms a, c and d.
The LCA will attempt to detect the presence of latent classes (the disease entities), creating patterns of association in the symptoms. As in factor analysis, the LCA can also be used to classify case according to their maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
class membership.
Because the criterion for solving the LCA is to achieve latent classes within which there is no longer any association of one symptom with another (because the class is the disease which causes their association, and the set of diseases a patient has (or class a case is a member of) causes the symptom association, the symptoms will be "conditionally independent", i.e., conditional on class membership, they are no longer related.
Related methods
As in much of statistics, there are a large number of methods with distinct names and uses, which share a common relationship. Cluster analysis is, like LCA, used to discover taxon-like groups of cases in data. Multivariate mixture estimation (MME) is applicable to continuous data, and assumes that such data arise from a mixture of distributions: imagine a set of heights arising from a mixture of men and women. If a Multivariate mixture estimation is constrained so that measures must be uncorrelated within each distribution it termed latent profile analysis. Modified to handle discrete data, this constrained analysis is known as LCA. Discrete latent trait models further constrain the classes to formed from segments of a single dimension: essentially allocating members to classes on that dimension: an example would be assigning cases to social classes on a dimension of ability or merit.As a practical instance, the variables could be multiple choice
Multiple choice
Multiple choice is a form of assessment in which respondents are asked to select the best possible answer out of the choices from a list. The multiple choice format is most frequently used in educational testing, in market research, and in elections-- when a person chooses between multiple...
items of a political questionnaire. The data in this case consists of a N-way contingency table
Contingency table
In statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
with answers to the items for a number of respondents. In this example, the latent variable refers to political opinion and the latent classes to political groups. Given group membership, the conditional probabilities specify the chance certain answers are chosen.
Within each latent class, the observed variables are statistically independent. This is an important aspect. Usually the observed variables are statistically dependent. By introducing the latent variable, independence is restored in the sense that within classes variables are independent (local independence
Local independence
Local independence is the underlying assumption of latent variable models.The observed items are conditionally independent of each other given an individual score on the latent variable. This means that the latent variable explains why the observed items are related to another...
). We then say that the association between the observed variables is explained by the classes of the latent variable (McCutcheon, 1987).
In one form the latent class model is written as
-
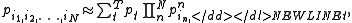
where T is the number of latent classes and pt are the so-called recruitment
or unconditional probabilities that should sum to one.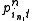
are the
marginal or conditional probabilities.
For a two-way latent class model the form is
This two-way model is related to probabilistic latent semantic analysisProbabilistic latent semantic analysisProbabilistic latent semantic analysis , also known as probabilistic latent semantic indexing is a statistical technique for the analysis of two-mode and co-occurrence data. PLSA evolved from latent semantic analysis, adding a sounder probabilistic model...
and non-negative matrix factorization.
Software
- R package poLCA for Latent Class Analysis and Latent Class Regression Modeling
- PROC LCA & PROC LTA Free SAS Procedures for Latent Class Analysis and Latent Transition Analysis
- Mplus
- Lem
- R package e1071 contains LCA
External links
- The Methodology Center, Latent Class Analysis, a research center at Penn State, free software, FAQ
- John Uebersax, Latent Class Analysis, 2006. A web-site with bibliography, software, links and FAQ for latent class analysis
-
