Contingency table
Encyclopedia
In statistics
, a contingency table (also referred to as cross tabulation
or cross tab) is a type of table
in a matrix
format that displays the (multivariate) frequency distribution
of the variables. It is often used to record and analyze the relation between two or more categorical variables.
The term contingency table was first used by Karl Pearson
in "On the Theory of Contingency and Its Relation to Association and Normal Correlation", part of the Drapers' Company Research Memoirs Biometric Series I published in 1904.
A crucial problem of multivariate statistics is finding (direct-)dependence structure underlying the variables contained in high dimensional contingency tables. If some of the conditional independence
s are revealed, then even the storage of the data can be done in a smarter way (see Lauritzen (2002)). In order to do this one can use information theory
concepts, which gain the information only from the distribution of probability, which can be expressed easily from the contingency table by the relative frequencies.
(right- or left-handed). Further suppose that 100 individuals are randomly sampled from a very large population as part of a study of sex differences in handedness. A contingency table can be created to display the numbers of individuals who are male and right-handed, male and left-handed, female and right-handed, and female and left-handed. Such a contingency table is shown below.
The numbers of the males, females, and right- and left-handed individuals are called marginal totals
. The grand total, i.e., the total number of individuals represented in the contingency table, is the number in the bottom right corner.
The table allows us to see at a glance that the proportion of men who are right-handed is about the same as the proportion of women who are right-handed although the proportions are not identical. The significance
of the difference between the two proportions can be assessed with a variety of statistical tests including Pearson's chi-squared test
, the G-test
, Fisher's exact test
, and Barnard's test
, provided the entries in the table represent individuals randomly sampled from the population about which we want to draw a conclusion. If the proportions of individuals in the different columns vary significantly between rows (or vice versa), we say that there is a contingency between the two variables. In other words, the two variables are not independent. If there is no contingency, we say that the two variables are independent.
The example above is the simplest kind of contingency table, a table in which each variable has only two levels; this is called a 2 x 2 contingency table. In principle, any number of rows and columns may be used. There may also be more than two variables, but higher order contingency tables are difficult to represent on paper. The relation between ordinal variables, or between ordinal and categorical variables, may also be represented in contingency tables, although such a practice is rare.
defined by
where χ2 is derived from Pearson's chi-squared test
, and N is the grand total of observations. φ varies from 0 (corresponding to no association between the variables) to 1 or -1 (complete association or complete inverse association). This coefficient can only be calculated for frequency data represented in 2 x 2 tables. φ can reach a minimum value -1.00 and a maximum value of 1.00 only when every marginal proportion is equal to .50 (and two diagonal cells are empty). Otherwise, the phi coefficient cannot reach those minimal and maximal values.
Alternatives include the tetrachoric correlation coefficient
(also only applicable to 2 × 2 tables), the contingency coefficient C, and Cramér's V
.
C suffers from the disadvantage that it does not reach a maximum of 1 or the minimum of -1; the highest it can reach in a 2 x 2 table is .707; the maximum it can reach in a 4 × 4 table is 0.870. It can reach values closer to 1 in contingency tables with more categories. It should, therefore, not be used to compare associations among tables with different numbers of categories. Moreover, it does not apply to asymmetrical tables (those where the numbers of row and columns are not equal).
The formulae for the C and V coefficients are:
k being the number of rows or the number of columns, whichever is less.
C can be adjusted so it reaches a maximum of 1 when there is complete association in a table of any number of rows and columns by dividing C by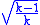
(recall that C only applies to tables in which the number of rows is equal to the number of columns and therefore equal to k).
The tetrachoric correlation coefficient
assumes that the variable underlying each dichotomous measure is normally distributed. The tetrachoric correlation coefficient provides "a convenient measure of [the Pearson product-moment] correlation when graduated measurements have been reduced to two categories." The tetrachoric correlation should not be confused with the Pearson product-moment correlation coefficient
computed by assigning, say, values 0 and 1 to represent the two levels of each variable (which is mathematically equivalent to the phi coefficient). An extension of the tetrachoric correlation to tables involving variables with more than two levels is the polychoric correlation
coefficient.
The Lambda coefficient is a measure of the strength of association of the cross tabulations when the variables are measured at the nominal level
. Values range from 0 (no association) to 1 (the theoretical maximum possible association). Asymmetric lambda measures the percentage improvement in predicting the dependent variable. Symmetric lambda measures the percentage improvement when prediction is done in both directions.
The uncertainty coefficient
is another measure for variables at the nominal level.
All of the following measures are used for variables at the ordinal level
. The values range from -1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a contingency table (also referred to as cross tabulation
Cross tabulation
Cross tabulation is the process of creating a contingency table from the multivariate frequency distribution of statistical variables. Heavily used in survey research, cross tabulations can be produced by a range of statistical packages, including some that are specialised for the task. Survey...
or cross tab) is a type of table
Table
Table or Tables may refer to:* Table * Table * Deliberative procedures:** Table , deferral or commencement of consideration** Table , contrasting usages* Tables , a class of board games...
in a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
format that displays the (multivariate) frequency distribution
Frequency distribution
In statistics, a frequency distribution is an arrangement of the values that one or more variables take in a sample. Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and in this way, the table summarizes the distribution of...
of the variables. It is often used to record and analyze the relation between two or more categorical variables.
The term contingency table was first used by Karl Pearson
Karl Pearson
Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
in "On the Theory of Contingency and Its Relation to Association and Normal Correlation", part of the Drapers' Company Research Memoirs Biometric Series I published in 1904.
A crucial problem of multivariate statistics is finding (direct-)dependence structure underlying the variables contained in high dimensional contingency tables. If some of the conditional independence
Conditional independence
In probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
s are revealed, then even the storage of the data can be done in a smarter way (see Lauritzen (2002)). In order to do this one can use information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
concepts, which gain the information only from the distribution of probability, which can be expressed easily from the contingency table by the relative frequencies.
Example
Suppose that we have two variables, sex (male or female) and handednessHandedness
Handedness is a human attribute defined by unequal distribution of fine motor skills between the left and right hands. An individual who is more dexterous with the right hand is called right-handed and one who is more skilled with the left is said to be left-handed...
(right- or left-handed). Further suppose that 100 individuals are randomly sampled from a very large population as part of a study of sex differences in handedness. A contingency table can be created to display the numbers of individuals who are male and right-handed, male and left-handed, female and right-handed, and female and left-handed. Such a contingency table is shown below.
| Right-handed | Left-handed | Totals | |
|---|---|---|---|
| Males | 43 | 9 | 52 |
| Females | 44 | 4 | 48 |
| Totals | 87 | 13 | 100 |
The numbers of the males, females, and right- and left-handed individuals are called marginal totals
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
. The grand total, i.e., the total number of individuals represented in the contingency table, is the number in the bottom right corner.
The table allows us to see at a glance that the proportion of men who are right-handed is about the same as the proportion of women who are right-handed although the proportions are not identical. The significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
of the difference between the two proportions can be assessed with a variety of statistical tests including Pearson's chi-squared test
Pearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
, the G-test
G-test
In statistics, G-tests are likelihood-ratio or maximum likelihood statistical significance tests that are increasingly being used in situations where chi-squared tests were previously recommended....
, Fisher's exact test
Fisher's exact test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
, and Barnard's test
Barnard's test
In statistics, Barnard's test is an exact test of the null hypothesis of independence of rows and columns in a contingency table. It is an alternative to Fisher's exact test but is more time-consuming to compute...
, provided the entries in the table represent individuals randomly sampled from the population about which we want to draw a conclusion. If the proportions of individuals in the different columns vary significantly between rows (or vice versa), we say that there is a contingency between the two variables. In other words, the two variables are not independent. If there is no contingency, we say that the two variables are independent.
The example above is the simplest kind of contingency table, a table in which each variable has only two levels; this is called a 2 x 2 contingency table. In principle, any number of rows and columns may be used. There may also be more than two variables, but higher order contingency tables are difficult to represent on paper. The relation between ordinal variables, or between ordinal and categorical variables, may also be represented in contingency tables, although such a practice is rare.
Measures of association
The degree of association between the two variables can be assessed by a number of coefficients: the simplest is the phi coefficientPhi coefficient
In statistics, the phi coefficient is a measure of association for two binary variables introduced by Karl Pearson. This measure is similar to the Pearson correlation coefficient in its interpretation...
defined by
-
,
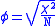where χ2 is derived from Pearson's chi-squared test
Pearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
, and N is the grand total of observations. φ varies from 0 (corresponding to no association between the variables) to 1 or -1 (complete association or complete inverse association). This coefficient can only be calculated for frequency data represented in 2 x 2 tables. φ can reach a minimum value -1.00 and a maximum value of 1.00 only when every marginal proportion is equal to .50 (and two diagonal cells are empty). Otherwise, the phi coefficient cannot reach those minimal and maximal values.
Alternatives include the tetrachoric correlation coefficient
Polychoric correlation
In statistics, polychoric correlation is a technique for estimating the correlation between two theorised normally distributed continuous latent variables, from two observed ordinal variables. Tetrachoric correlation is a special case of the polychoric correlation applicable when both observed...
(also only applicable to 2 × 2 tables), the contingency coefficient C, and Cramér's V
Cramér's V
In statistics, Cramér's V is a popular measure of association between two nominal variables, giving a value between 0 and +1...
.
C suffers from the disadvantage that it does not reach a maximum of 1 or the minimum of -1; the highest it can reach in a 2 x 2 table is .707; the maximum it can reach in a 4 × 4 table is 0.870. It can reach values closer to 1 in contingency tables with more categories. It should, therefore, not be used to compare associations among tables with different numbers of categories. Moreover, it does not apply to asymmetrical tables (those where the numbers of row and columns are not equal).
The formulae for the C and V coefficients are:
-
and
-
,
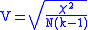k being the number of rows or the number of columns, whichever is less.
C can be adjusted so it reaches a maximum of 1 when there is complete association in a table of any number of rows and columns by dividing C by
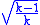(recall that C only applies to tables in which the number of rows is equal to the number of columns and therefore equal to k).The tetrachoric correlation coefficient
Polychoric correlation
In statistics, polychoric correlation is a technique for estimating the correlation between two theorised normally distributed continuous latent variables, from two observed ordinal variables. Tetrachoric correlation is a special case of the polychoric correlation applicable when both observed...
assumes that the variable underlying each dichotomous measure is normally distributed. The tetrachoric correlation coefficient provides "a convenient measure of [the Pearson product-moment] correlation when graduated measurements have been reduced to two categories." The tetrachoric correlation should not be confused with the Pearson product-moment correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
computed by assigning, say, values 0 and 1 to represent the two levels of each variable (which is mathematically equivalent to the phi coefficient). An extension of the tetrachoric correlation to tables involving variables with more than two levels is the polychoric correlation
Polychoric correlation
In statistics, polychoric correlation is a technique for estimating the correlation between two theorised normally distributed continuous latent variables, from two observed ordinal variables. Tetrachoric correlation is a special case of the polychoric correlation applicable when both observed...
coefficient.
The Lambda coefficient is a measure of the strength of association of the cross tabulations when the variables are measured at the nominal level
Level of measurement
The "levels of measurement", or scales of measure are expressions that typically refer to the theory of scale types developed by the psychologist Stanley Smith Stevens. Stevens proposed his theory in a 1946 Science article titled "On the theory of scales of measurement"...
. Values range from 0 (no association) to 1 (the theoretical maximum possible association). Asymmetric lambda measures the percentage improvement in predicting the dependent variable. Symmetric lambda measures the percentage improvement when prediction is done in both directions.
The uncertainty coefficient
Uncertainty coefficient
In statistics, the uncertainty coefficient, also called entropy coefficient or Theil's U, is a measure of nominal association. It was first introduced by Henri Theil and is based on the concept of information entropy. Suppose we have samples of two random variables, i and j...
is another measure for variables at the nominal level.
All of the following measures are used for variables at the ordinal level
Level of measurement
The "levels of measurement", or scales of measure are expressions that typically refer to the theory of scale types developed by the psychologist Stanley Smith Stevens. Stevens proposed his theory in a 1946 Science article titled "On the theory of scales of measurement"...
. The values range from -1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.
- Gamma testGamma test (statistics)In statistics, a gamma test tests the strength of association of the cross tabulated data when both variables are measured at the ordinal level. It makes no adjustment for either table size or ties. Values range from −1 to +1...
: No adjustment for either table size or ties. - Kendall tau: Adjustment for ties.
- Tau b: For square tables.
- Tau c: For rectangular tables.
See also
- The pivotPivot tableIn data processing, a pivot table is a data summarization tool found in data visualization programs such as spreadsheets or business intelligence software. Among other functions, pivot-table tools can automatically sort, count, total or give the average of the data stored in one table or spreadsheet...
operation in spreadsheet software can be used to generate a contingency table from sampling data. - TPL TablesTPL TablesTPL Tables is a cross tabulation system used to generate statistical tables for analysis or publication.- Background / History :TPL Tables has its roots in the Table Producing Language system, developed at the Bureau of Labor Statistics in the 1970s and early 1980s to run on IBM mainframes. It...
is a tool for generating and printing cross tabs. - The iterative proportional fittingIterative proportional fittingThe iterative proportional fitting procedure is an iterative algorithm for estimating cell values of a contingency table such that the marginal totals remain fixed and the estimated table decomposes into an outer...
procedure essentially manipulates contingency tables to match altered joint distributions or marginal sums. - The multivariate statisticsMultivariate statisticsMultivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
in special multivariate discrete probability distributions. Some procedures used in this context can be used in dealing with contingency tables.
External links
- On-line analysis of contingency tables: calculator with examples
- Interactive cross tabulation, chi-squared independent test & tutorial
- Fisher and chi-squared calculator of 2 × 2 contingency table
- More Correlation Coefficients
- Nominal Association: Phi, Contingency Coefficient, Tschuprow's T, Cramer's V, Lambda, Uncertainty Coefficient
- Customer Insight com Cross Tabulation
- The POWERMUTT Project: IV. DISPLAYING CATEGORICAL DATA
- StATS: Steves Attempt to Teach Statistics Odds ratio versus relative risk (January 9, 2001)
- [ftp://ftp.cdc.gov/pub/Software/epi_info/EIHAT_WEB/Lesson5AnalysisCreatingStatistics.pdf Epi Info Community Health Assessment Tutorial Lesson 5 Analysis: Creating Statistics]