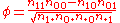Phi coefficient
Encyclopedia
In statistics
, the phi coefficient (also referred to as the "mean square contingency coefficient" and denoted by φ or rφ) is a measure of association for two binary variables introduced by Karl Pearson
. This measure is similar to the Pearson correlation coefficient in its interpretation. In fact, a Pearson correlation coefficient estimated for two binary variables will return the phi coefficient. The square of the Phi coefficient is related to the chi-squared
statistic
for a 2×2 contingency table
(see Pearson's chi-squared test
)
where n is the total number of observations. Two binary variables are considered positively associated if most of the data falls along the diagonal cells. In contrast, two binary variables are considered negatively associated if most of the data falls off the diagonal. If we have a 2×2 table for two random variables x and y
where n11, n10, n01, n00, are non-negative "cell cell counts" that sum to n, the total number of observations. The phi coefficient that describes the association of x and y is
Phi is related to the point-biserial correlation coefficient
and Cohen's d and estimates the extent of the relationship between two variables (2 x 2).
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the phi coefficient (also referred to as the "mean square contingency coefficient" and denoted by φ or rφ) is a measure of association for two binary variables introduced by Karl Pearson
Karl Pearson
Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
. This measure is similar to the Pearson correlation coefficient in its interpretation. In fact, a Pearson correlation coefficient estimated for two binary variables will return the phi coefficient. The square of the Phi coefficient is related to the chi-squared
Chi-squared
In statistics, the term chi-squared has different uses:*chi-squared distribution, a continuous probability distribution;*chi-squared statistic, a statistic used in some statistical tests;...
statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
for a 2×2 contingency table
Contingency table
In statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
(see Pearson's chi-squared test
Pearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
)
where n is the total number of observations. Two binary variables are considered positively associated if most of the data falls along the diagonal cells. In contrast, two binary variables are considered negatively associated if most of the data falls off the diagonal. If we have a 2×2 table for two random variables x and y
| y = 1 | y = 0 | total | |
| x = 1 | 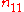 |
 |
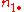 |
| x = 0 |  |
 |
 |
| total |  |
 |
 |
where n11, n10, n01, n00, are non-negative "cell cell counts" that sum to n, the total number of observations. The phi coefficient that describes the association of x and y is
Phi is related to the point-biserial correlation coefficient
Point-biserial correlation coefficient
The point biserial correlation coefficient is a correlation coefficient used when one variable is dichotomous; Y can either be "naturally" dichotomous, like gender, or an artificially dichotomized variable. In most situations it is not advisable to artificially dichotomize variables...
and Cohen's d and estimates the extent of the relationship between two variables (2 x 2).
Maximum values
Although computationally the Pearson correlation coefficient reduces to the phi coefficient in the 2×2 case, the interpretation of a Pearson correlation coefficient and phi coefficient must be taken cautiously. The Pearson correlation coefficient ranges from −1 to +1, where ±1 indicates perfect agreement or disagreement, and 0 indicates no relationship. The phi coefficient has a maximum value that is determined by the distribution of the two variables. If both have a 50/50 split, values of phi will range from −1 to +1. See Davenport El-Sanhury (1991) for a thorough discussion.See also
- Contingency tableContingency tableIn statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
- Matthews correlation coefficientMatthews Correlation CoefficientThe Matthews correlation coefficient is used in machine learning as a measure of the quality of binary classifications. It takes into account true and false positives and negatives and is generally regarded as a balanced measure which can be used even if the classes are of very different sizes...
- Cramér's V, a similar measure of association between nominal variables.