
Lefschetz pencil
Encyclopedia
In mathematics
, a Lefschetz pencil is a construction in algebraic geometry
considered by Solomon Lefschetz
, in order to analyse the algebraic topology
of an algebraic variety
V. A pencil here is a particular kind of linear system of divisors
on V, namely a one-parameter family, parametrised by the projective line
. This means that in the case of a complex algebraic variety V, a Lefschetz pencil is something like a fibration
over the Riemann sphere
; but with two qualifications about singularity.
The first point comes up if we assume that V is given as a projective variety, and the divisors on V are hyperplane section
s. Suppose given hyperplanes H and H′, spanning the pencil — in other words, H is given by L = 0 and H′ by L′= 0 for linear forms L and L′, and the general hyperplane section is V intersected with
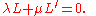
Then the intersection J of H with H′ has codimension
two. There is a rational mapping

which is in fact well-defined only outside the points on the intersection of J with V. To make a well-defined mapping, some blowing up
must be applied to V.
The second point is that the fibers may themselves 'degenerate' and acquire singular points
(where Bertini's lemma applies, the general hyperplane section will be smooth). A Lefschetz pencil restricts the nature of the acquired singularities, so that the topology may be analysed by the vanishing cycle
method. The fibres with singularities are required to have a unique quadratic singularity, only.
It has been shown that Lefschetz pencils exist in characteristic zero. They apply in ways similar to, but more complicated than, Morse functions on smooth manifolds.
Simon Donaldson
has found a role for Lefschetz pencils in symplectic topology
, leading to more recent research interest in them.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lefschetz pencil is a construction in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
considered by Solomon Lefschetz
Solomon Lefschetz
Solomon Lefschetz was an American mathematician who did fundamental work on algebraic topology, its applications to algebraic geometry, and the theory of non-linear ordinary differential equations.-Life:...
, in order to analyse the algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
of an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V. A pencil here is a particular kind of linear system of divisors
Linear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
on V, namely a one-parameter family, parametrised by the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
. This means that in the case of a complex algebraic variety V, a Lefschetz pencil is something like a fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
over the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
; but with two qualifications about singularity.
The first point comes up if we assume that V is given as a projective variety, and the divisors on V are hyperplane section
Hyperplane section
In mathematics, a hyperplane section of a subset X of projective space Pn is the intersection of X with some hyperplane H — in other words we look at the subset XH of those elements x of X that satisfy the single linear condition L = 0 defining H as a linear subspace...
s. Suppose given hyperplanes H and H′, spanning the pencil — in other words, H is given by L = 0 and H′ by L′= 0 for linear forms L and L′, and the general hyperplane section is V intersected with
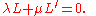
Then the intersection J of H with H′ has codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
two. There is a rational mapping
Rational mapping
In mathematics, in particular the subfield of algebraic geometry, a rational map is a kind of partial function between algebraic varieties. This article uses the convention that varieties are irreducible.-Formal definition:...

which is in fact well-defined only outside the points on the intersection of J with V. To make a well-defined mapping, some blowing up
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
must be applied to V.
The second point is that the fibers may themselves 'degenerate' and acquire singular points
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
(where Bertini's lemma applies, the general hyperplane section will be smooth). A Lefschetz pencil restricts the nature of the acquired singularities, so that the topology may be analysed by the vanishing cycle
Vanishing cycle
In mathematics, vanishing cycles are studied in singularity theory and other parts of algebraic geometry. They are those homology cycles of a smooth fiber in a family which vanish in the singular fiber....
method. The fibres with singularities are required to have a unique quadratic singularity, only.
It has been shown that Lefschetz pencils exist in characteristic zero. They apply in ways similar to, but more complicated than, Morse functions on smooth manifolds.
Simon Donaldson
Simon Donaldson
Simon Kirwan Donaldson FRS , is an English mathematician known for his work on the topology of smooth four-dimensional manifolds. He is now Royal Society research professor in Pure Mathematics and President of the Institute for Mathematical Science at Imperial College London...
has found a role for Lefschetz pencils in symplectic topology
Symplectic topology
Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
, leading to more recent research interest in them.
External links
- Gompf, Robert; What is a Lefschetz pencil?; (PDF) Notices of the American Mathematical Society; vol. 52, no. 8 (September 2005).
- Gompf, Robert; The Topology of Symplectic Manifolds (PDF) pp.10-12.

