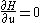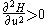Legendre-Clebsch condition
Encyclopedia
In the calculus of variations
the Legendre-Clebsch condition is a second-order condition which a solution of the Euler-Lagrange equation
must satisfy in order to be a maximum (and not a minimum or another kind of extremal).
For the problem of maximizing
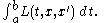
the condition is
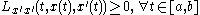
In optimal control
, the situation is more complicated because of the possibility of a singular solution
. The generalized Legendre-Clebsch condition, also known as convexity, is a sufficient condition for local optimality such that when the linear sensitivity of the Hamiltonian to changes in u is zero, i.e.,
The Hessian of the Hamiltonian is positive definite along the trajectory of the solution:
In words, the generalized LC condition guarantees that over a singular arc, the Hamiltonian is minimized.
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
the Legendre-Clebsch condition is a second-order condition which a solution of the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
must satisfy in order to be a maximum (and not a minimum or another kind of extremal).
For the problem of maximizing
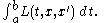
the condition is
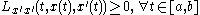
In optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
, the situation is more complicated because of the possibility of a singular solution
Singular control
In optimal control, problems of singular control are problems that are difficult to solve because a straightforward application of Pontryagin's minimum principle fails to yield a complete solution. Only a few such problems have been solved, such as Merton's portfolio problem in financial economics...
. The generalized Legendre-Clebsch condition, also known as convexity, is a sufficient condition for local optimality such that when the linear sensitivity of the Hamiltonian to changes in u is zero, i.e.,
The Hessian of the Hamiltonian is positive definite along the trajectory of the solution:
In words, the generalized LC condition guarantees that over a singular arc, the Hamiltonian is minimized.