Leibniz rule (generalized product rule)
Encyclopedia
In calculus
, the general Leibniz rule, named after Gottfried Leibniz
, generalizes the product rule
. It states that if f and g are n-times differentiable functions, then the nth derivative of the product fg is given by
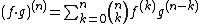
where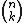
is the binomial coefficient
.
This can be proved by using the product rule and mathematical induction
.
With the multi-index notation the rule states more generally:
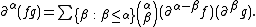
This formula can be used to derive a formula that computes the symbol of the composition of differential operators. In fact, let P and Q be differential operators (with coefficients that are differentiable sufficiently many times) and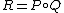
. Since R is also a differential operator, the symbol of R is given by:
A direct computation now gives:
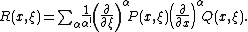
This formula is usually known as the Leibniz formula. It is used to define the composition in the space of symbols, thereby inducing the ring structure.
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the general Leibniz rule, named after Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, generalizes the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
. It states that if f and g are n-times differentiable functions, then the nth derivative of the product fg is given by
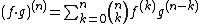
where
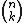is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
This can be proved by using the product rule and mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.
With the multi-index notation the rule states more generally:
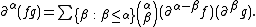
This formula can be used to derive a formula that computes the symbol of the composition of differential operators. In fact, let P and Q be differential operators (with coefficients that are differentiable sufficiently many times) and
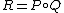. Since R is also a differential operator, the symbol of R is given by:A direct computation now gives:
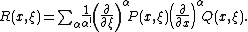
This formula is usually known as the Leibniz formula. It is used to define the composition in the space of symbols, thereby inducing the ring structure.
See also
- Derivation (abstract algebra)Derivation (abstract algebra)In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
- Differential algebraDifferential algebraIn mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
- Product ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
- DerivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...