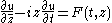Lewy's example
Encyclopedia
In the mathematical
study of partial differential equation
s, Lewy's example is a celebrated example, due to Hans Lewy
, of a linear partial differential equation with no solutions. It shows that the analog of the Cauchy–Kovalevskaya theorem does not hold in the smooth category.
The original example is not explicit, since it employs the Hahn–Banach theorem
, but there since have been various explicit examples of the same nature found by Harold Jacobowitz.
The Malgrange–Ehrenpreis theorem
states (roughly) that linear partial differential equations with constant coefficients always have at least one solution; Lewy's example shows that this result cannot be extended to linear partial differential equations with polynomial coefficients.
Lewy constructs this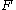 using the following result:
using the following result:
This may be construed as a non-existence theorem by taking φ to be merely a smooth function. Lewy's example takes this latter equation and in a sense translates its non-solvability to every point of ℝ×ℂ. The method of proof uses a Baire category argument, so in a certain precise sense almost all equations of this form are unsolvable.
later found that the even simpler equation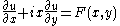
depending on 2 real variables x and y sometimes has no solutions. This is almost the simplest possible partial differential operator with non-constant coefficients.
comes equipped with a chain complex
of differential operators, formally similar to the Dolbeault complex on a complex manifold
, called the -complex. The Dolbeault complex admits a version of the Poincaré lemma. In the language of sheaves
-complex. The Dolbeault complex admits a version of the Poincaré lemma. In the language of sheaves
, this means that the Dolbeault complex is exact. The Lewy example, however, shows that the -complex is almost never exact.
-complex is almost never exact.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, Lewy's example is a celebrated example, due to Hans Lewy
Hans Lewy
Hans Lewy was an American mathematician, known for his work on partial differential equations and on the theory of functions of several complex variables....
, of a linear partial differential equation with no solutions. It shows that the analog of the Cauchy–Kovalevskaya theorem does not hold in the smooth category.
The original example is not explicit, since it employs the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, but there since have been various explicit examples of the same nature found by Harold Jacobowitz.
The Malgrange–Ehrenpreis theorem
Malgrange–Ehrenpreis theorem
In mathematics, the Malgrange–Ehrenpreis theorem states that every non-zero linear differential operator with constant coefficients has a Green's function...
states (roughly) that linear partial differential equations with constant coefficients always have at least one solution; Lewy's example shows that this result cannot be extended to linear partial differential equations with polynomial coefficients.
The Example
The statement is as follows- On ℝ×ℂ, there exists a smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
complex-valued function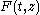 such that the differential equation
such that the differential equation
- admits no solution on any open set. Note that if
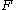 is analytic then the Cauchy–Kovalevskaya theorem implies there exists a solution.
is analytic then the Cauchy–Kovalevskaya theorem implies there exists a solution.
Lewy constructs this
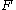 using the following result:
using the following result:
- On ℝ×ℂ, suppose that
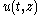 is a function satisfying, in a neighborhood of the origin,
is a function satisfying, in a neighborhood of the origin,
- for some C1 function φ. Then φ must be real-analytic in a (possibly smaller) neighborhood of the origin.
This may be construed as a non-existence theorem by taking φ to be merely a smooth function. Lewy's example takes this latter equation and in a sense translates its non-solvability to every point of ℝ×ℂ. The method of proof uses a Baire category argument, so in a certain precise sense almost all equations of this form are unsolvable.
later found that the even simpler equation
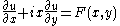
depending on 2 real variables x and y sometimes has no solutions. This is almost the simplest possible partial differential operator with non-constant coefficients.
Significance for CR manifolds
A CR manifoldCR manifold
In mathematics, a CR manifold is a differentiable manifold together with a geometric structure modeled on that of a real hypersurface in a complex vector space, or more generally modeled on an edge of a wedge....
comes equipped with a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
of differential operators, formally similar to the Dolbeault complex on a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
, called the
 -complex. The Dolbeault complex admits a version of the Poincaré lemma. In the language of sheaves
-complex. The Dolbeault complex admits a version of the Poincaré lemma. In the language of sheavesSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
, this means that the Dolbeault complex is exact. The Lewy example, however, shows that the
 -complex is almost never exact.
-complex is almost never exact.