Light orbital angular momentum
Encyclopedia
The light orbital angular momentum (OAM) is the component of angular momentum of a light beam that is dependent on the field spatial distribution, and not on the polarization
. It can be further split into an internal and an external OAM. The internal OAM is an origin-independent angular momentum of a light beam that can be associated with a helical or twisted wavefront
. The external OAM is the origin-dependent angular momentum that can be obtained as cross product
of the light beam position
(center of the beam) and its total linear momentum.
, and hence it can be also attributed an external angular momentum 
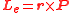. This external angular momentum depends on the choice of the origin of the coordinate system. If one chooses the origin at the beam axis and the beam is cylindrically symmetric (at least in its momentum distribution), the external angular momentum will vanish. The external angular momentum is a form of OAM, because it is unrelated with polarization
and depends on the spatial distribution of the optical field
.
A more interesting example of OAM is the internal OAM appearing when a paraxial light beam is in a so-called “helical mode”. Helical modes of the electromagnetic field
are characterized by a wavefront
that is shaped as a helix
, with an optical vortex
in the center, at the beam axis (see figure). The helical modes are characterized by an integer number
, positive or negative. If 
, the mode is not helical and the wavefronts are multiple disconnected surfaces, for example a sequence of parallel planes (from which the name “plane wave”). If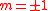 
, the handedness determined by the sign of 
. If 
, the wavefront
is shaped as
distinct wavefront is a single helical surface, with a step length equal to the wavelength
, and a still intertwined helices, with a step length of each helix surface equal to 
, and a handedness given by the sign of 
. The integer 
is also the so-called “topological charge” of the optical vortex
. Light beams that are in a helical mode carry nonzero OAM.
In this figure, the first column shows the beam wavefront shape. The second column is the optical phase distribution in a beam cross-section, shown in false colors. The third column is the light intensity distribution in a beam cross-section (with a dark vortex core at the center).
The beam photons in this case have an OAM of
directed along the beam axis. This OAM is origin-independent.
An example of optical modes having a helical wavefront
is provided by the set of Laguerre-Gaussian modes.
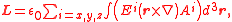
where
and 
are the electric field
and the vector potential
, respectively,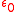
is the vacuum permittivity and we are using SI units. The 
-superscripted symbols denote the cartesian components of the corresponding vectors.
For a monochromatic wave this expression can be transformed into the following one :
This expression is generally nonvanishing when the wave is not cylindrically symmetric. In particular, in a quantum theory, individual photons may have the following values of the OAM:
The corresponding wave functions (eigenfunctions of OAM operator) have the following general expression:
where
is the cylindrical coordinate. As mentioned in the Introduction, this expression corresponds to waves having a helical wavefront (see figure above), with an optical vortex in the center, at the beam axis.
Polarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
. It can be further split into an internal and an external OAM. The internal OAM is an origin-independent angular momentum of a light beam that can be associated with a helical or twisted wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
. The external OAM is the origin-dependent angular momentum that can be obtained as cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of the light beam position
Position
Position may refer to:* Position , a player role within a team* Position , the orientation of a baby prior to birth* Position , a mathematical identification of relative location...
(center of the beam) and its total linear momentum.
Introduction
A beam of light carries a linear momentum, and hence it can be also attributed an external angular momentum 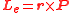. This external angular momentum depends on the choice of the origin of the coordinate system. If one chooses the origin at the beam axis and the beam is cylindrically symmetric (at least in its momentum distribution), the external angular momentum will vanish. The external angular momentum is a form of OAM, because it is unrelated with polarizationPolarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
and depends on the spatial distribution of the optical field
Optical field
The optical field is a term used in physics and vector calculus to designate the electric field shown as E in the electromagnetic wave equation which can be derived from Maxwell's Equations...
.
A more interesting example of OAM is the internal OAM appearing when a paraxial light beam is in a so-called “helical mode”. Helical modes of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
are characterized by a wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
that is shaped as a helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
, with an optical vortex
Optical vortex
An optical vortex is a zero of an optical field, a point of zero intensity. Research into the properties of vortices has thrived since a comprehensive paper by Nye and Berry, in 1974, described the basic properties of "dislocations in wave trains"...
in the center, at the beam axis (see figure). The helical modes are characterized by an integer number
, positive or negative. If , the mode is not helical and the wavefronts are multiple disconnected surfaces, for example a sequence of parallel planes (from which the name “plane wave”). If 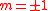, the handedness determined by the sign of . If , the wavefrontWavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
is shaped as
distinct wavefront is a single helical surface, with a step length equal to the wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, and a still intertwined helices, with a step length of each helix surface equal to , and a handedness given by the sign of . The integer is also the so-called “topological charge” of the optical vortexOptical vortex
An optical vortex is a zero of an optical field, a point of zero intensity. Research into the properties of vortices has thrived since a comprehensive paper by Nye and Berry, in 1974, described the basic properties of "dislocations in wave trains"...
. Light beams that are in a helical mode carry nonzero OAM.
In this figure, the first column shows the beam wavefront shape. The second column is the optical phase distribution in a beam cross-section, shown in false colors. The third column is the light intensity distribution in a beam cross-section (with a dark vortex core at the center).
The beam photons in this case have an OAM of
directed along the beam axis. This OAM is origin-independent.An example of optical modes having a helical wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
is provided by the set of Laguerre-Gaussian modes.
Mathematical expressions for the orbital angular momentum of light
The classical expression of the orbital angular momentum in the paraxial limit is the following: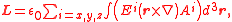where
and are the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
, respectively,
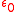is the vacuum permittivity and we are using SI units. The -superscripted symbols denote the cartesian components of the corresponding vectors.For a monochromatic wave this expression can be transformed into the following one :
This expression is generally nonvanishing when the wave is not cylindrically symmetric. In particular, in a quantum theory, individual photons may have the following values of the OAM:
The corresponding wave functions (eigenfunctions of OAM operator) have the following general expression:
where
is the cylindrical coordinate. As mentioned in the Introduction, this expression corresponds to waves having a helical wavefront (see figure above), with an optical vortex in the center, at the beam axis.