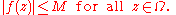Lindelöf's theorem
Encyclopedia
In mathematics
, Lindelöf's theorem is a result in complex analysis
named after the Finnish
mathematician
Ernst Leonard Lindelöf
. It states that a holomorphic function
on a half-strip in the complex plane
that is bounded
on the boundary
of the strip and does not grow "too fast" in the unbounded direction of the strip must remain bounded on the whole strip. The result is useful in the study of the Riemann zeta function, and is a special case of the Phragmén–Lindelöf principle. Also, see Hadamard three-lines theorem
.
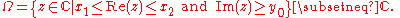
Suppose that ƒ is holomorphic (i.e. analytic
) on Ω and that there are constants M, A and B such that

and
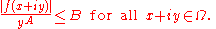
Then f is bounded by M on all of Ω:
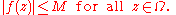
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Lindelöf's theorem is a result in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
named after the Finnish
Finland
Finland , officially the Republic of Finland, is a Nordic country situated in the Fennoscandian region of Northern Europe. It is bordered by Sweden in the west, Norway in the north and Russia in the east, while Estonia lies to its south across the Gulf of Finland.Around 5.4 million people reside...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Ernst Leonard Lindelöf
Ernst Leonard Lindelöf
Ernst Leonard Lindelöf, was a Finnish topologist after whom Lindelöf spaces are named; he was the son of Leonard Lorenz Lindelöf and brother of the philologist Uno Lorenz Lindelöf....
. It states that a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on a half-strip in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
that is bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the strip and does not grow "too fast" in the unbounded direction of the strip must remain bounded on the whole strip. The result is useful in the study of the Riemann zeta function, and is a special case of the Phragmén–Lindelöf principle. Also, see Hadamard three-lines theorem
Hadamard three-lines theorem
In complex analysis, a branch of mathematics, theHadamard three-lines theorem, named after the French mathematician Jacques Hadamard, is a result about the behaviour of holomorphic functions defined in regions bounded by parallel lines in the complex plane....
.
Statement of the theorem
Let Ω be a half-strip in the complex plane: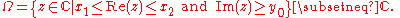
Suppose that ƒ is holomorphic (i.e. analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
) on Ω and that there are constants M, A and B such that

and
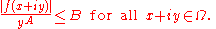
Then f is bounded by M on all of Ω: