Hadamard three-lines theorem
Encyclopedia
In complex analysis
, a branch of mathematics
, the
Hadamard three-lines theorem, named after the French mathematician Jacques Hadamard
, is a result about the behaviour of holomorphic function
s defined in regions bounded by parallel lines in the complex plane.
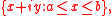
holomorphic in the interior of the strip and continuous on the whole strip. Then, if
log M(x) is a convex function on [a, b].
In other words, if
with 
, then
by
Thus
on the edges of the strip.
The maximum modulus principle
can be applied to
in the strip in the form due to Phragmén and Lindelöf.
It shows that the same inequality holds throughout the strip.
This inequality is equivalent to the three lines theorem.
for a bounded continuous function
on an
annulus
, holomorphic in the interior. Indeed applying the theorem to
shows that, if
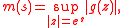
then
is a convex function of s.
The three-line theorem also holds for functions with values in a Banach space
and plays an important rôle in complex interpolation theory, It can be used to prove Hölder's inequality
for measurable functions
where
, by considering the function
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the
Hadamard three-lines theorem, named after the French mathematician Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
, is a result about the behaviour of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s defined in regions bounded by parallel lines in the complex plane.
Statement
Let f(z) be a bounded function of z = x + iy defined on the strip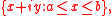holomorphic in the interior of the strip and continuous on the whole strip. Then, if
log M(x) is a convex function on [a, b].
In other words, if
with , thenProof
Define byThus
on the edges of the strip.The maximum modulus principle
Maximum modulus principle
In mathematics, the maximum modulus principle in complex analysis states that if f is a holomorphic function, then the modulus |f| cannot exhibit a true local maximum that is properly within the domain of f....
can be applied to
in the strip in the form due to Phragmén and Lindelöf.
It shows that the same inequality holds throughout the strip.
This inequality is equivalent to the three lines theorem.
Applications
The three-line theorem can be used to prove the Hadamard three-circle theoremHadamard three-circle theorem
In complex analysis, a branch of mathematics, theHadamard three-circle theorem is a result about the behavior of holomorphic functions.Let f be a holomorphic function on the annulusr_1\leq\left| z\right| \leq r_3....
for a bounded continuous function
on anannulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
, holomorphic in the interior. Indeed applying the theorem toshows that, if
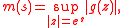
then
is a convex function of s.The three-line theorem also holds for functions with values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and plays an important rôle in complex interpolation theory, It can be used to prove Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
for measurable functions
where
, by considering the function