In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the maximum modulus principle in complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

 states that if f is a holomorphic function

Holomorphic function

In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...

, then the modulus

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

  cannot exhibit a true local maximum that is properly within the domain

Domain (mathematics)

In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...

 of f.

In other words, either f is a constant function

Constant function

In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...

, or, for any point z₀ inside the domain of f there exist other points arbitrarily close to z₀ at which |f | takes larger values.

Formal statement

Let f be a function holomorphic on some connected open

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

 D of the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

 C and taking complex values. If z₀ is a point in D such that
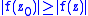
for all z in a neighborhood of z₀, then the function f is constant on D.

Sketch of the proof

One uses the equality

log f(z) = log |f(z)| + i arg f(z)

for complex natural logarithm

Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

s to deduce that log |f(z)| is a harmonic function

Harmonic function

In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....

. Since z₀ is a local maximum for this function also, it follows from the maximum principle

Maximum principle

In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...

 that |f(z)| is constant. Then, using the Cauchy-Riemann equations

Cauchy-Riemann equations

In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...

 we show that f(z)=0, and thus that f(z) is constant as well.

Another proof works by using Gauss's mean value theorem to "force" all points within overlapping open disks to assume the same value. The disks are laid such that their centers form a polygonal path from the value where f(z) is maximized to any other point in the domain, while being totally contained within the domain. Thus the existence of a maximum value implies that all the values in the domain are the same, thus f(z) is constant.

By switching to the reciprocal

Multiplicative inverse

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...

, we can get the minimum modulus principle. It states that if f is holomorphic within a bounded domain D, continuous up to the boundary

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

 of D, and non-zero at all points, then the modulus |f (z)| takes its minimum value on the boundary of D.

Alternatively, the maximum modulus principle can be viewed as a special case of the open mapping theorem

Open mapping theorem (complex analysis)

In complex analysis, the open mapping theorem states that if U is a connected open subset of the complex plane C and f : U → C is a non-constant holomorphic function, then f is an open map .The open mapping theorem points to the sharp difference between holomorphy and real-differentiability...

, which states that a nonconstant holomorphic function maps open sets to open sets. If |f| attains a local maximum at a, then the image of a sufficiently small open neighborhood of a cannot be open. Therefore, f is constant.

Physical Interpretation

A physical interpretation of this principle comes from the heat equation. That is, since log |f(z)| is harmonic, it is thus the steady state of a heat flow on the region D. Suppose a strict maximum was attained on the interior of D, the heat at this maximum would be dispersing to the points around it, which would contradict the assumption that this represents the steady state of a system.

Applications

The maximum modulus principle has many uses in complex analysis, and may be used to prove the following:

• The fundamental theorem of algebra
  Fundamental theorem of algebra
  The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
  
  .
• Schwarz's lemma, a result which in turn has many generalisations and applications in complex analysis.
• The Phragmén–Lindelöf principle, an extension to unbounded domains.
• The Borel–Carathéodory theorem
  Borel–Carathéodory theorem
  In mathematics, the Borel–Carathéodory theorem in complex analysis shows that an analytic function may be bounded by its real part. It is an application of the maximum modulus principle. It is named for Émile Borel and Constantin Carathéodory....
  
  , which bounds an analytic function in terms of its real part.

External links

• The Maximum Modulus Principle by John H. Mathews