Open mapping theorem (complex analysis)
Encyclopedia
In complex analysis
, the open mapping theorem states that if U is a connected
open subset of the complex plane
C and f : U → C is a non-constant holomorphic function, then f is an open map (i.e. it sends open subsets of U to open subsets of C).
The open mapping theorem points to the sharp difference between holomorphy and real-differentiability. On the real line
, for example, the differentiable function f(x) = x2 is not an open map, as the image of the open interval (−1,1) is the half-open interval [0,1).
The theorem for example implies that a non-constant holomorphic function
cannot map an open disk onto a portion of any real line embedded in the complex plane. Images of holomorphic functions can be of dimension zero (if constant) or two (if non-constant) but never of dimension 1.
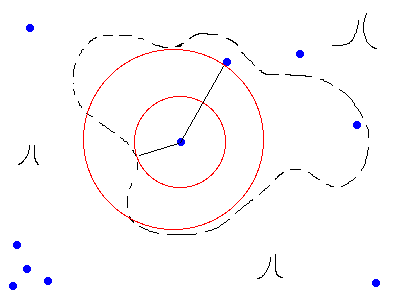Assume f:U → C is a non-constant holomorphic function and 
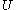is a connected open subset of the complex plane. We have to show that every point
in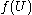
is an interior point of 
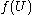, i.e. that every point in 
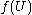is contained in a disk which is contained in 
.
Consider an arbitrary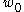
in 
. Then there exists a point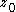 
in U such that 
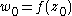. Since U is open, we can find 
such that the closed disk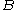 
around 
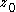with radius d is fully contained in U. Since U is connected and f is not constant on U, we then know that f is not constant on B because of Analytic continuation
. Consider the function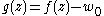
. Note that 
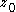is a root of the function.
We know that g(z) is not constant and holomorphic. The reciprocal of any holomorphic g(z) is meromorphic and has isolated poles. Thus the roots of holomorphic non-constant functions are isolated. In particular, the roots of g are isolated and by further decreasing the radius of the image disk d, we can assure that g(z) has only a single root in B.
The boundary of B is a circle and hence a compact set, and |g(z)| is a continuous function
, so the extreme value theorem
guarantees the existence of a minimum. Let e be the minimum of |g(z)| for z on the boundary of B, a positive number.
Denote by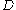
the disk around 
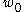with radius
e. By Rouché's theorem
, the function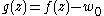
will have the same number of roots in B as 
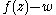for any 
within a distance 
of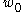 
. Thus, for every 
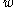in 
, there exists one (and only one) 
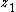in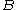 
so that 
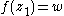. This means that the disk D is contained in 
.
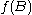The image of the ball B,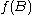
is a subset of the image of U, 
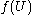. Thus 
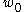is an interior point of the image of an open set by a holomorphic function 
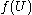. Since 
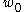was arbitrary in 
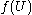we know that 
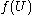is open. Since U was arbitrary, the function 
is open.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the open mapping theorem states that if U is a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
open subset of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C and f : U → C is a non-constant holomorphic function, then f is an open map (i.e. it sends open subsets of U to open subsets of C).
The open mapping theorem points to the sharp difference between holomorphy and real-differentiability. On the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, for example, the differentiable function f(x) = x2 is not an open map, as the image of the open interval (−1,1) is the half-open interval [0,1).
The theorem for example implies that a non-constant holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
cannot map an open disk onto a portion of any real line embedded in the complex plane. Images of holomorphic functions can be of dimension zero (if constant) or two (if non-constant) but never of dimension 1.
Proof
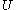is a connected open subset of the complex plane. We have to show that every pointPoint (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in
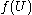is an interior point of 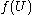, i.e. that every point in 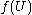is contained in a disk which is contained in .Consider an arbitrary
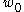in . Then there exists a point 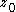in U such that 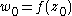. Since U is open, we can find such that the closed disk 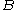around 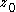with radius d is fully contained in U. Since U is connected and f is not constant on U, we then know that f is not constant on B because of Analytic continuationAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
. Consider the function
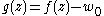. Note that 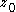is a root of the function.We know that g(z) is not constant and holomorphic. The reciprocal of any holomorphic g(z) is meromorphic and has isolated poles. Thus the roots of holomorphic non-constant functions are isolated. In particular, the roots of g are isolated and by further decreasing the radius of the image disk d, we can assure that g(z) has only a single root in B.
The boundary of B is a circle and hence a compact set, and |g(z)| is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, so the extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
guarantees the existence of a minimum. Let e be the minimum of |g(z)| for z on the boundary of B, a positive number.
Denote by
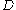the disk around 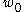with radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
e. By Rouché's theorem
Rouché's theorem
Rouché's theorem, named after , states that if the complex-valued functions f and g are holomorphic inside and on some closed contour K, with |g| ...
, the function
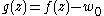will have the same number of roots in B as 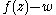for any within a distance of 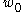. Thus, for every 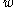in , there exists one (and only one) 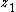in 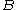so that 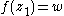. This means that the disk D is contained in 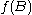.The image of the ball B,
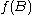is a subset of the image of U, 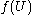. Thus 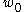is an interior point of the image of an open set by a holomorphic function 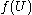. Since 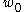was arbitrary in 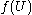we know that 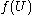is open. Since U was arbitrary, the function is open.