
Hadamard three-circle theorem
Encyclopedia
In complex analysis
, a branch of mathematics
, the
Hadamard three-circle theorem is a result about the behavior of holomorphic function
s.
Let be a holomorphic function on the annulus
be a holomorphic function on the annulus
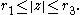
Let be the maximum
be the maximum
of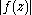 on the circle
on the circle
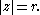 Then,
Then, 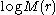 is a convex function
is a convex function
of the logarithm
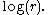 Moreover, if
Moreover, if 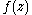 is not of the form
is not of the form  for some constants
for some constants
 and
and  , then
, then 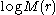 is strictly convex as a function of
is strictly convex as a function of 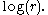
The conclusion of the theorem
can be restated as
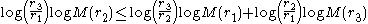
for any three concentric circles of radii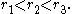
and Edmund Landau
attribute the theorem to Jacques Hadamard
, writing in 1896; Hadamard published no proof.
The theorem can also be deduced directly from Hadamard's three-lines theorem
.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the
Hadamard three-circle theorem is a result about the behavior of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s.
Let
 be a holomorphic function on the annulus
be a holomorphic function on the annulusAnnulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
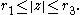
Let
 be the maximum
be the maximumMaxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of
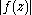 on the circle
on the circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
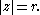 Then,
Then, 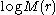 is a convex function
is a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
of the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
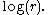 Moreover, if
Moreover, if 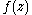 is not of the form
is not of the form  for some constants
for some constantsCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
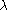 and
and  , then
, then 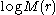 is strictly convex as a function of
is strictly convex as a function of 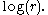
The conclusion of the theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
can be restated as
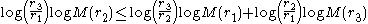
for any three concentric circles of radii
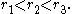
History
A statement and proof for the theorem was given by J.E. Littlewood in 1912, but he attributes it to no one in particular, stating it as a known theorem. Harald BohrHarald Bohr
Harald August Bohr was a Danish mathematician and football player. After receiving his doctorate in 1910, Bohr became an eminent mathematician, founding the field of almost periodic functions. His brother was the Nobel Prize-winning physicist Niels Bohr...
and Edmund Landau
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
attribute the theorem to Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
, writing in 1896; Hadamard published no proof.
Proof
The three circles theorem follows from the fact that for any real a, the function Re log(zaf(z)) is harmonic between two circles, and therefore takes its maximum value on one of the circles. The theorem follows by choosing the constant a so that this harmonic function has the same maximum value on both circles.The theorem can also be deduced directly from Hadamard's three-lines theorem
Hadamard three-lines theorem
In complex analysis, a branch of mathematics, theHadamard three-lines theorem, named after the French mathematician Jacques Hadamard, is a result about the behaviour of holomorphic functions defined in regions bounded by parallel lines in the complex plane....
.
See also
- maximum principleMaximum principleIn mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
- logarithmically convex functionLogarithmically convex functionIn mathematics, a function f defined on a convex subset of a real vector space and taking positive values is said to be logarithmically convex if \log f is a convex function of x....
- Hardy's theoremHardy's theoremIn mathematics, Hardy's theorem is a result in complex analysis describing the behavior of holomorphic functions.Let f be a holomorphic function on the open ball centered at zero and radius R in the complex plane, and assume that f is not a constant function...
- Hadamard three-lines theoremHadamard three-lines theoremIn complex analysis, a branch of mathematics, theHadamard three-lines theorem, named after the French mathematician Jacques Hadamard, is a result about the behaviour of holomorphic functions defined in regions bounded by parallel lines in the complex plane....
- Borel–Carathéodory theoremBorel–Carathéodory theoremIn mathematics, the Borel–Carathéodory theorem in complex analysis shows that an analytic function may be bounded by its real part. It is an application of the maximum modulus principle. It is named for Émile Borel and Constantin Carathéodory....
- Phragmén–Lindelöf principle

