
Linearly disjoint
Encyclopedia
In mathematics, algebra
s A, B over a field k inside some field extension of k (e.g., universal field) are said to be linearly disjoint over k if the following equivalent conditions are met:
of k (e.g., universal field) are said to be linearly disjoint over k if the following equivalent conditions are met:
Note that, since every subalgebra of is a domain, (i) implies
is a domain, (i) implies 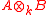 is a domain (in particular reduced
is a domain (in particular reduced
).
One also has: A, B are linearly disjoint over k if and only if subfields of generated by
generated by 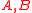 , resp. are linearly disjoint over k. (cf. tensor product of fields
, resp. are linearly disjoint over k. (cf. tensor product of fields
)
Suppose A, B are linearly disjoint over k. If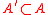 ,
,  are subalgebras, then
are subalgebras, then  and
and  are linearly disjoint over k. Conversely, if any finitely generated subalgebras of algebras A, B are linearly disjoint, then A, B are linearly disjoint (since the condition involves only finite sets of elements.)
are linearly disjoint over k. Conversely, if any finitely generated subalgebras of algebras A, B are linearly disjoint, then A, B are linearly disjoint (since the condition involves only finite sets of elements.)
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
s A, B over a field k inside some field extension
 of k (e.g., universal field) are said to be linearly disjoint over k if the following equivalent conditions are met:
of k (e.g., universal field) are said to be linearly disjoint over k if the following equivalent conditions are met:
- (i) The map
 induced by
induced by  is injective.
is injective. - (ii) Any k-basis of A remains linearly independent over B.
- (iii) If
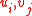 are k-bases for A, B, then the products
are k-bases for A, B, then the products 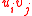 are linearly independent over k.
are linearly independent over k.
Note that, since every subalgebra of
 is a domain, (i) implies
is a domain, (i) implies 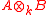 is a domain (in particular reduced
is a domain (in particular reducedReduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
).
One also has: A, B are linearly disjoint over k if and only if subfields of
 generated by
generated by 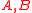 , resp. are linearly disjoint over k. (cf. tensor product of fields
, resp. are linearly disjoint over k. (cf. tensor product of fieldsTensor product of fields
In abstract algebra, the theory of fields lacks a direct product: the direct product of two fields, considered as a ring is never itself a field. On the other hand it is often required to 'join' two fields K and L, either in cases where K and L are given as subfields of a larger field M, or when K...
)
Suppose A, B are linearly disjoint over k. If
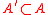 ,
,  are subalgebras, then
are subalgebras, then  and
and  are linearly disjoint over k. Conversely, if any finitely generated subalgebras of algebras A, B are linearly disjoint, then A, B are linearly disjoint (since the condition involves only finite sets of elements.)
are linearly disjoint over k. Conversely, if any finitely generated subalgebras of algebras A, B are linearly disjoint, then A, B are linearly disjoint (since the condition involves only finite sets of elements.)

