Linearly ordered group
Encyclopedia
In abstract algebra
a linearly ordered or totally ordered group is an ordered group
G such that the order relation
"≤" is total
. This means that the following statements hold for all a, b, c ∈ G:
In analogy with ordinary numbers, we call an element c of an ordered group positive if 0 ≤ c and c ≠ 0, where "0" here denotes the identity element
of the group (not necessarily the familiar zero of the real numbers). The set of positive elements in a group is often denoted with G+.
For every element a of a linearly ordered group G either a ∈ G+, or −a ∈ G+, or a = 0. If a linearly ordered group G is not trivial (i.e. 0 is not its only element), then G+ is infinite. Therefore, every nontrivial linearly ordered group is infinite.
If a is an element of a linearly ordered group G, then the absolute value
of a, denoted by |a|, is defined to be:
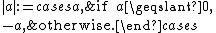
If in addition the group G is abelian
, then for any a, b ∈ G the triangle inequality
is satisfied: |a + b| ≤ |a| + |b|.
F. W. Levi showed that an abelian group
admits a linear order if and only if it is torsion-free .
Otto Hölder
showed that every linearly ordered group satisfying an Archimedean property
is isomorphic
to a subgroup of the additive group of real number
s, .
If we write the archimedean l.o. group multiplicatively, this may be shown by considering the dedekind completion,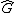
of the closure of an l.o. group under 
th roots. We endow this space with the usual topology of a linear order, and then it can be shown that for each 
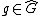the exponential maps 
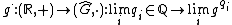are well defined order preserving/reversing, topological group isomorphisms.
Completing an l.o. group can be difficult in the non-archimedean case. In these cases, one may classify a group by its rank: which is related to the order type of the largest sequence of convex subgroups.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
a linearly ordered or totally ordered group is an ordered group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
G such that the order relation
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
"≤" is total
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
. This means that the following statements hold for all a, b, c ∈ G:
- if a ≤ b and b ≤ a then a = b (antisymmetry)
- if a ≤ b and b ≤ c then a ≤ c (transitivity)
- a ≤ b or b ≤ a (totality)
- the order relation is translation invariant: if a ≤ b then a + c ≤ b + c and c + a ≤ c + b.
In analogy with ordinary numbers, we call an element c of an ordered group positive if 0 ≤ c and c ≠ 0, where "0" here denotes the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of the group (not necessarily the familiar zero of the real numbers). The set of positive elements in a group is often denoted with G+.
For every element a of a linearly ordered group G either a ∈ G+, or −a ∈ G+, or a = 0. If a linearly ordered group G is not trivial (i.e. 0 is not its only element), then G+ is infinite. Therefore, every nontrivial linearly ordered group is infinite.
If a is an element of a linearly ordered group G, then the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of a, denoted by |a|, is defined to be:
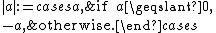
If in addition the group G is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, then for any a, b ∈ G the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
is satisfied: |a + b| ≤ |a| + |b|.
F. W. Levi showed that an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
admits a linear order if and only if it is torsion-free .
Otto Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
showed that every linearly ordered group satisfying an Archimedean property
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to a subgroup of the additive group of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, .
If we write the archimedean l.o. group multiplicatively, this may be shown by considering the dedekind completion,
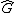of the closure of an l.o. group under th roots. We endow this space with the usual topology of a linear order, and then it can be shown that for each 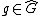the exponential maps 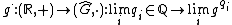are well defined order preserving/reversing, topological group isomorphisms.Completing an l.o. group can be difficult in the non-archimedean case. In these cases, one may classify a group by its rank: which is related to the order type of the largest sequence of convex subgroups.