
Liouville's formula
Encyclopedia
In mathematics
, Liouville's formula is an equation that expresses the determinant
of a square-matrix solution of a first-order system of homogeneous linear differential equation
s in terms of the sum of the diagonal coefficients of the system. The formula is named after the French
mathematician
Joseph Liouville
.
Liouville's formula is a generalization of Abel's identity
and can be used to prove it. Since Liouville's formula relates the different linearly independent
solutions of the system of differential equations, it can help to find one solution from the other(s), see the example application below.

on an interval
I of the real line
, where A(x) for x ∈ I denotes a square matrix of dimension n with real
or complex
entries. Let Φ denote a matrix-valued solution on I, meaning that each Φ(x) is a square matrix of dimension n with real or complex entries and the derivative
satisfies
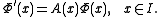
Let
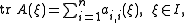
denote the trace
of A(ξ) = (ai,j (ξ))i,j ∈ {1,...,n}, the sum of its diagonal entries. If the trace of A is a continuous function
, then the determinant of Φ satisfies

for all x and x0 in I.
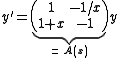
on the open interval I = (0, ∞). Assume that the easy solution
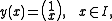
is already found. Let

denote another solution, then

is a square-matrix-valued solution of the above differential equation. Since the trace of A(x) is zero for all x ∈ I, Liouville's formula implies that the determinant
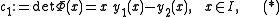
is actually a constant independent of x. Writing down the first component of the differential equation for y, we obtain using (*) that
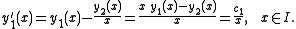
Therefore, by integration, we see that
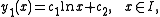
involving the natural logarithm
and the constant of integration c2. Solving equation (*) for y2(x) and substituting for y1(x) gives
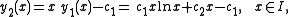
which is the general solution for y. With the special choice c1 = 0 and c2 = 1 we recover the easy solution we started with, the choice c1 = 1 and c2 = 0 yields a linearly independent solution. Therefore,

is a so-called fundamental solution of the system.
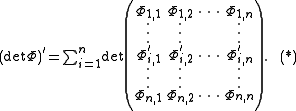
Since the matrix-valued solution Φ satisfies the equation Φ' = AΦ, we have for every entry of the matrix Φ'
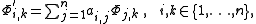
or for the entire row

When we subtract from the i th row the linear combination
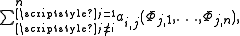
of all the other rows, then the value of the determinant remains unchanged, hence
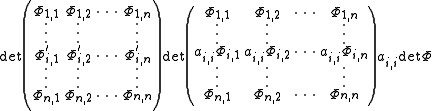
for every i ∈ {1,...,n} by the linearity of the determinant with respect to every row. Hence

by (*) and the definition of the trace. It remains to show that this representation of the derivative implies Liouville's formula.
Fix x0 ∈ I. Since the trace of A is assumed to be continuous function on I, it is bounded on every closed and bounded subinterval of I and therefore integrable, hence
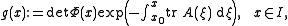
is a well defined function. Differentiating both sides, using the product rule, the chain rule
, the derivative of the exponential function
and the fundamental theorem of calculus
, we obtain
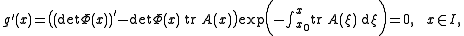
due to the derivative in (**). Therefore, g has to be constant on I, because otherwise we would obtain a contradiction to the mean value theorem
(applied separately to the real and imaginary part in the complex-valued case). Since g(x0) = det Φ(x0), Liouville's formula follows by solving the definition of g for det Φ(x).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Liouville's formula is an equation that expresses the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a square-matrix solution of a first-order system of homogeneous linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s in terms of the sum of the diagonal coefficients of the system. The formula is named after the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
.
Liouville's formula is a generalization of Abel's identity
Abel's identity
In mathematics, Abel's identity is an equation that expresses the Wronskian of two homogeneous solutions of a second-order linear ordinary differential equation in terms of a coefficient of the original differential equation.The relation can be generalised to nth-order linear ordinary differential...
and can be used to prove it. Since Liouville's formula relates the different linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
solutions of the system of differential equations, it can help to find one solution from the other(s), see the example application below.
Statement of Liouville's formula
Consider the n-dimensional first-order homogeneous linear differential equation
on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
I of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, where A(x) for x ∈ I denotes a square matrix of dimension n with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
entries. Let Φ denote a matrix-valued solution on I, meaning that each Φ(x) is a square matrix of dimension n with real or complex entries and the derivative
Matrix calculus
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices, where it defines the matrix derivative. This notation was to describe systems of differential equations, and taking derivatives of matrix-valued functions with respect...
satisfies
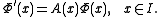
Let
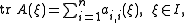
denote the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of A(ξ) = (ai,j (ξ))i,j ∈ {1,...,n}, the sum of its diagonal entries. If the trace of A is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, then the determinant of Φ satisfies

for all x and x0 in I.
Example application
This example illustrates how Liouville's formula can help to find the general solution of a first-order system of homogeneous linear differential equations. Consider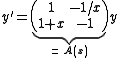
on the open interval I = (0, ∞). Assume that the easy solution
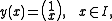
is already found. Let

denote another solution, then

is a square-matrix-valued solution of the above differential equation. Since the trace of A(x) is zero for all x ∈ I, Liouville's formula implies that the determinant
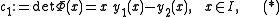
is actually a constant independent of x. Writing down the first component of the differential equation for y, we obtain using (*) that
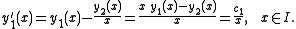
Therefore, by integration, we see that
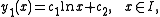
involving the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
and the constant of integration c2. Solving equation (*) for y2(x) and substituting for y1(x) gives
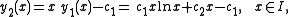
which is the general solution for y. With the special choice c1 = 0 and c2 = 1 we recover the easy solution we started with, the choice c1 = 1 and c2 = 0 yields a linearly independent solution. Therefore,

is a so-called fundamental solution of the system.
Proof of Liouville's formula
We omit the argument x for brevity. By the Leibniz formula for determinants, the derivative of the determinant of Φ = (Φi,j )i,j ∈ {0,...,n} can be calculated by differentiating one row at a time and taking the sum, i.e.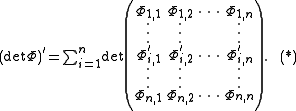
Since the matrix-valued solution Φ satisfies the equation Φ' = AΦ, we have for every entry of the matrix Φ'
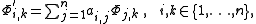
or for the entire row

When we subtract from the i th row the linear combination
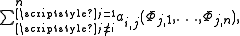
of all the other rows, then the value of the determinant remains unchanged, hence
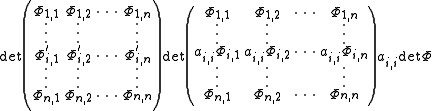
for every i ∈ {1,...,n} by the linearity of the determinant with respect to every row. Hence

by (*) and the definition of the trace. It remains to show that this representation of the derivative implies Liouville's formula.
Fix x0 ∈ I. Since the trace of A is assumed to be continuous function on I, it is bounded on every closed and bounded subinterval of I and therefore integrable, hence
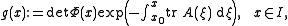
is a well defined function. Differentiating both sides, using the product rule, the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, the derivative of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
, we obtain
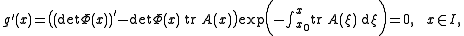
due to the derivative in (**). Therefore, g has to be constant on I, because otherwise we would obtain a contradiction to the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
(applied separately to the real and imaginary part in the complex-valued case). Since g(x0) = det Φ(x0), Liouville's formula follows by solving the definition of g for det Φ(x).

