Liouville field theory
Encyclopedia
In physics
, Liouville field theory (or simply Liouville theory) is a two-dimensional quantum field theory
whose classical equation of motion resembles the Joseph Liouville
's non-linear second order differential equation that appears in the classical geometrical problem of uniformizing Riemann surfaces .
The field theory is defined by the local action
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Liouville field theory (or simply Liouville theory) is a two-dimensional quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
whose classical equation of motion resembles the Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
's non-linear second order differential equation that appears in the classical geometrical problem of uniformizing Riemann surfaces .
The field theory is defined by the local action
-
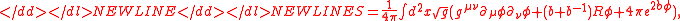
where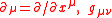
is the metric of the two-dimensional space on which the field theory is formulated, 
is the Ricci scalar of such space, and 
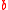is a real coupling constant. The field 
is consequently dubbed the Liouville field.
The equation of motion associated to this action is
-
where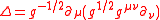
is the D'Alembert operatorD'Alembert operatorIn special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...
in such space (see also Laplace–Beltrami operator). In the case the metric of the space being the Euclidean metric, and using standard notation, it becomes the classical Liouville equation
-
Liouville field theory is a conformal field theoryConformal field theoryA conformal field theory is a quantum field theory that is invariant under conformal transformations...
that incarnates Weyl symmetry in a very special way . Its central charge
is given in terms of the parameter appearing in the action through the expression 
. Liouville theory appears in the context of string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
when trying to formulate a non-critical version of the theory in the path integralPath integralPath integral may refer to:* Line integral, the integral of a function along a curve* Functional integration, the integral of a functional over a space of curves...
approach . Also in the string theory context, if coupled to a free bosonic field Liouville field theory can be thought of as the theory describing string excitations in a two-dimensional space(time).
Liouville field theory is one of the best understood examples of what is called a non-rational conformal field theoryConformal field theoryA conformal field theory is a quantum field theory that is invariant under conformal transformations...
, for which some observables have been computed explicitly. Such is the case of two-point and three-point correlation functions of primary operators on the topology of the sphere, which were calculated in and . Explicit expressions for observables of the theory defined on other topologies, like the partition function on the torus and the one-point function on the disk, were also calculated in the recent years.
Liouville theory is also closely related to other problems in physics and mathematics, like two-dimensional quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
, two-dimensional string theory, three-dimensional general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
in negatively curved spaces, four-dimensional superconformal gauge theories, the uniformization problem of Riemann surfaces, and other problems in conformal mapping. It is also connected to other two-dimensional non-rational conformal field theories with affine symmetry, like the Wess–Zumino–Novikov–Witten theory for the group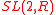
, and, besides, it can be regarded as a special case (namely the case 
) of the family of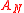 
Toda field theoriesToda field theoryIn the study of field theory and partial differential equations, a Toda field theory is derived from the following Lagrangian:...
. Liouville theory also admits supersymmetric extension. See the reviews of the subject and references therein and thereof.
-
-