List of number fields with class number one
Encyclopedia
This is an incomplete list of number fields with class number 1, ordered by their degree over Q.
It is believed that there are infinitely many such number fields, but this has not been proven.
of its ring of integers
.
Thus, a number field has class number 1 if and only if its ring of integers is a principal ideal domain
(and thus a unique factorization domain
).
d.
(complete until d = 100)
*: The narrow class number
is also 1 (see related sequence A003655 in OEIS).
Despite what would appear to be the case for these small values, not all prime numbers that are congruent to 1 modulo 4 appear on this list, notably the fields Q(√d) for and both have class number greater than 1 (in fact equal to 3 in both cases). The density of such primes for which Q(√d) does have class number 1 is conjectured to be nonzero, and in fact close to 76%,
however it is not even known for sure whether there are infinitely many real quadratic fields with class number 1.
(By definition, these also all have narrow class number 1.)
Cubic field
The first 60 totally real cubic fields (ordered by discriminant
) have class number one. In other words, all cubic fields of discriminant between 0 and 1944 (inclusively) have class number one. The next totally real cubic field (of discriminant 1957) has class number two. The discriminants less than 500 with class number one are:
Polynomials defining the first three are respectively:,,.
The first 30 complex cubic fields (ordered by discriminant) have class number one. That is, all cubic fields of discriminant between 0 and −268 (inclusively) have class number one. The next complex cubic field (of discriminant −283) has class number two. The negative discriminants less than 150 with class number one are:
Polynomials defining the first three are respectively:,,.
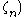have class number 1, the largest such n being 84.
On the other hand, the maximal real subfields ℚ(cos(2π/2n)) of the 2-power cyclotomic fields ℚ(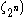
(where n is a positive integer) are known to have class number 1 for n≤7, and
it is conjectured that they have class number 1 for all n. Weber showed that these fields have odd class number. In 2009, Fukuda and Komatsu showed that the class numbers of these fields have no prime factor less than 107, and later improved this bound to 1.2×108. These fields are the n-th layers of the cyclotomic Z2-extension of Q. In the same year, Morisawa showed that the class numbers of the layers of the cyclotomic Z3-extension of Q have no prime factor less than 104. Coates has raised the question of whether, for all primes p, every layer of the cyclotomic Zp-extension of Q has class number 1.
It is believed that there are infinitely many such number fields, but this has not been proven.
Definition
The class number of a number field is by definition the order of the ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of its ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
.
Thus, a number field has class number 1 if and only if its ring of integers is a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
(and thus a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
).
Quadratic number fields
These are of the form K = Q(√d), for a square-free integerSquare-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
d.
Real quadratic fields
K is called real quadratic if d > 0. K has class number 1 for the following values of d :- 2*, 3, 5*, 6, 7, 11, 13*, 14, 17*, 19, 21, 22, 23, 29*, 31, 33, 37*, 38, 41*, 43, 46, 47, 53*, 57, 59, 61*, 62, 67, 69, 71, 73*, 77, 83, 86, 89*, 93, 94, 97*, ...
(complete until d = 100)
*: The narrow class number
Narrow class group
In algebraic number theory, the narrow class group of a number field K is a refinement of the class group of K that takes into account some information about embeddings of K into the field of real numbers.- Formal definition :...
is also 1 (see related sequence A003655 in OEIS).
Despite what would appear to be the case for these small values, not all prime numbers that are congruent to 1 modulo 4 appear on this list, notably the fields Q(√d) for and both have class number greater than 1 (in fact equal to 3 in both cases). The density of such primes for which Q(√d) does have class number 1 is conjectured to be nonzero, and in fact close to 76%,
however it is not even known for sure whether there are infinitely many real quadratic fields with class number 1.
Imaginary quadratic fields
K has class number 1 exactly for the following negative values of d:- −1, −2, −3, −7, −11, −19, −43, −67, −163.
(By definition, these also all have narrow class number 1.)
Cubic fieldCubic fieldIn mathematics, specifically the area of algebraic number theory, a cubic field is an algebraic number field of degree three.-Definition:If K is a field extension of the rational numbers Q of degree [K:Q] = 3, then K is called a cubic field...
s
The first 60 totally real cubic fields (ordered by discriminantDiscriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
) have class number one. In other words, all cubic fields of discriminant between 0 and 1944 (inclusively) have class number one. The next totally real cubic field (of discriminant 1957) has class number two. The discriminants less than 500 with class number one are:
- 49, 81, 148, 169, 229, 257, 316, 321, 361, 404, 469, 473.
Polynomials defining the first three are respectively:,,.
The first 30 complex cubic fields (ordered by discriminant) have class number one. That is, all cubic fields of discriminant between 0 and −268 (inclusively) have class number one. The next complex cubic field (of discriminant −283) has class number two. The negative discriminants less than 150 with class number one are:
- −23, −31, −44, −59, −76, −83, −87, −104, −107, −108, −116, −135, −139, −140.
Polynomials defining the first three are respectively:,,.
Higher-degree number fields
For x a root of one of the equations below, the fields Q(x) have class number 1.- X4 + X3 - 2X - 1
- X5 + X4 - 3X3 - 2X2 + X - 1
- X5 - 2X4 - 2X3 + 2 X2 + X + 1
Cyclotomic fields
Only a finite number of the cyclotomic fields ℚ(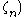 have class number 1, the largest such n being 84.On the other hand, the maximal real subfields ℚ(cos(2π/2n)) of the 2-power cyclotomic fields ℚ(
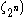(where n is a positive integer) are known to have class number 1 for n≤7, andit is conjectured that they have class number 1 for all n. Weber showed that these fields have odd class number. In 2009, Fukuda and Komatsu showed that the class numbers of these fields have no prime factor less than 107, and later improved this bound to 1.2×108. These fields are the n-th layers of the cyclotomic Z2-extension of Q. In the same year, Morisawa showed that the class numbers of the layers of the cyclotomic Z3-extension of Q have no prime factor less than 104. Coates has raised the question of whether, for all primes p, every layer of the cyclotomic Zp-extension of Q has class number 1.