
Lobb numbers
Encyclopedia
The Lobb numbers, named after Andrew Lobb, are a natural generalization of the Catalan numbers, originally introduced to give a simple inductive proof
of the formula for the nth Catalan number.
The Lobb numbers depend on the input of two non-negative integers m and n with n ≥ m ≥ 0. The (m, n)th Lobb number Lm,n is given in terms of binomial coefficient
s by
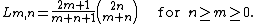
For m = 0, L0,n coincides with the nth Catalan number. The Lobb numbers solve the combinatorial
problem that asks for the number of ways in which n + m values of +1 and n − m values of −1 can be arranged so that no partial sum is negative (when m = 0 this is a restatement of Catalan's problem
). Equivalently, Lm,n is the number of ways that n + m opening parentheses and n − m closing parentheses can be arranged so that the resulting string is the prefix of (or, when m = 0, the entirety of) a valid string of balanced parentheses
.
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
of the formula for the nth Catalan number.
The Lobb numbers depend on the input of two non-negative integers m and n with n ≥ m ≥ 0. The (m, n)th Lobb number Lm,n is given in terms of binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s by
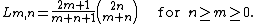
For m = 0, L0,n coincides with the nth Catalan number. The Lobb numbers solve the combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
problem that asks for the number of ways in which n + m values of +1 and n − m values of −1 can be arranged so that no partial sum is negative (when m = 0 this is a restatement of Catalan's problem
Catalan's problem
In mathematics, Catalan's problem asks the number of ways n + 1 factors can be completely parenthesized by n pairs of parentheses...
). Equivalently, Lm,n is the number of ways that n + m opening parentheses and n − m closing parentheses can be arranged so that the resulting string is the prefix of (or, when m = 0, the entirety of) a valid string of balanced parentheses
Dyck language
In the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...
.

