
Local Langlands conjectures
Encyclopedia
In mathematics, the local Langlands conjectures, introduced by , are part of the Langlands program
. They describe a correspondence between representations of the Weil group
of a local field
and representations of algebraic group
s over the local field, generalizing local class field theory from abelian Galois group
s to non-abelian Galois groups.
irreducible smooth representations of GL1(K).
For every Frobenius semisimple complex n-dimensional Weil–Deligne representations ρ of the Weil group of F there is an L-function L(s,ρ) and a local ε-factor
ε(s,ρ,ψ) (depending on a character ψ of F).
Smooth irreducible representations are automatically admissible.
The Bernstein–Zelevinsky classification
reduces the classification of irreducible smooth representations to cuspidal representations.
For every irreducible admissible complex representation π there is an L-function L(s,π) and a local ε-factor ε(s,π,ψ) (depending on a character ψ of F). More generally, if there are two irreducible admissible representations π and π' of general linear groups there are local Rankin–Selberg convolution L-functions L(s,π×π') and ε-factors ε(s,π×π',ψ).
described the irreducible admissible representations of general linear groups over local fields.
verified the local Langlands conjectures for GL2 in the case when the residue field does not have characteristic 2. In this case the representations of the Weil group are all of cyclic or dihedral type. classified the smooth irreducible representations of GL2(F) when F has odd residue characteristic (see also ), and claimed incorrectly that the classification for even residue characteristic differs only insignifictanly from the odd residue characteristic case.
pointed out that when the residue field has characteristic 2, there are some extra exceptional 2-dimensional representations of the Weil group whose image in PGL2(C) is of tetrahedral or octahedral type. (For global Langlands conjectures, 2-dimensional representations can also be of icosaheral type, but this cannot happen in the local case as the Galois groups are solvable.)
proved the local Langlands conjectures for the general linear group GL2(K) over the 2-adic numbers, and over local fields containing a cube root of unity.
proved the local Langlands conjectures for the general linear group GL2(K) over all local fields.
and gave expositions of the proof.
proved the local Langlands conjectures for the general linear group GLn(K) for positive characteristic local fields K. gave an exposition of their work.
proved the local Langlands conjectures for the general linear group GLn(K) for characteristic 0 local fields K. gave another proof. and gave expositions of their work.
proved the Langlands conjectures for groups over the archimedean local fields R and C by giving the Langlands classification
of their irreducible admissible representations (up to infinitesimal equivalence), or, equivalently, of their irreducible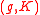 -modules
-modules
.
proved the local Langlands conjectures for the symplectic similitude group GSp(4) and used that in to deduce it for the symplectic group
Sp(4).
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
. They describe a correspondence between representations of the Weil group
Weil group
In mathematics, a Weil group, introduced by , is a modification of the absolute Galois group of a local or global field, used in class field theory. For such a field F, its Weil group is a profinite group generally denoted WF...
of a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
and representations of algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s over the local field, generalizing local class field theory from abelian Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
s to non-abelian Galois groups.
Local Langlands conjectures for GL1
The local Langlands conjectures for GL1(K) follow from (and are essentially equivalent to) local class field theory. More precisely the Artin map gives an isomorphism from the group GL1(K)= K* to the abelianization of the Weil group. In particular irreducible smooth representations of GL1(K) are 1-dimensional as the group is abelian, so can be identified with homomorphisms of the Weil group to GL1(C). This gives the Langlands correspondence between homomorphisms of the Weil group to GL1(C) andirreducible smooth representations of GL1(K).
Representations of the Weil group
Representations of the Weil group do not quite correspond to irreducible smooth representations of general linear groups. To get a bijection, one has to slightly modify the notion of a representation of the Weil group, to something called a Weil–Deligne representation. This consists of a representation of the Weil group on a vector space V together with a nilpotent endomorphism N of V such that wNw−1=||w||N, or equivalently a representation of the Weil–Deligne group. In addition the representation of the Weil group should have an open kernel, and should be (Frobenius) semisimple.For every Frobenius semisimple complex n-dimensional Weil–Deligne representations ρ of the Weil group of F there is an L-function L(s,ρ) and a local ε-factor
Langlands–Deligne local constant
In mathematics, the Langlands–Deligne local constant is an elementary function associated with a representation of the Weil group of a local field...
ε(s,ρ,ψ) (depending on a character ψ of F).
Representations of GLn(F)
The representations of GLn(F) appearing in the local Langlands correspondence are smooth irreducible complex representations.- "Smooth" means that every vector is fixed by some open subgroup.
- "Irreducible" means that the representation is nonzero and has no subrepresentations other than 0 and itself.
Smooth irreducible representations are automatically admissible.
The Bernstein–Zelevinsky classification
Bernstein–Zelevinsky classification
In mathematics, the Bernstein–Zelevinsky classification, introduced by and , classifies the irreducible complex smooth representations of a general linear group over a local field in terms of cuspidal representations....
reduces the classification of irreducible smooth representations to cuspidal representations.
For every irreducible admissible complex representation π there is an L-function L(s,π) and a local ε-factor ε(s,π,ψ) (depending on a character ψ of F). More generally, if there are two irreducible admissible representations π and π' of general linear groups there are local Rankin–Selberg convolution L-functions L(s,π×π') and ε-factors ε(s,π×π',ψ).
described the irreducible admissible representations of general linear groups over local fields.
Local Langlands conjectures for GL2
The local Langlands conjecture for GL2 of a local field says that there is a (unique) bijection π from 2-dimensional semisimple Deligne representations of the Weil group to irreducible smooth representations of GL2(F) that preserves L-functions, ε-factors, and commutes with twisting by characters of F*.verified the local Langlands conjectures for GL2 in the case when the residue field does not have characteristic 2. In this case the representations of the Weil group are all of cyclic or dihedral type. classified the smooth irreducible representations of GL2(F) when F has odd residue characteristic (see also ), and claimed incorrectly that the classification for even residue characteristic differs only insignifictanly from the odd residue characteristic case.
pointed out that when the residue field has characteristic 2, there are some extra exceptional 2-dimensional representations of the Weil group whose image in PGL2(C) is of tetrahedral or octahedral type. (For global Langlands conjectures, 2-dimensional representations can also be of icosaheral type, but this cannot happen in the local case as the Galois groups are solvable.)
proved the local Langlands conjectures for the general linear group GL2(K) over the 2-adic numbers, and over local fields containing a cube root of unity.
proved the local Langlands conjectures for the general linear group GL2(K) over all local fields.
and gave expositions of the proof.
Local Langlands conjectures for GLn
The local Langlands conjectures for general linear groups state that there are unique bijections π ↔ ρπ from equivalence classes of irreducible admissible representations π of GLn(F) to equivalence classes of continuous Frobenius semisimple complex n-dimensional Weil–Deligne representations ρπ of the Weil group of F, that preserve L-functions and ε-factors of pairs of representations, and coincide with the Artin map for 1-dimensional representations. In other words,- L(s,ρπ⊗ρπ') = L(s,π×π')
- ε(s,ρπ⊗ρπ',ψ) = ε(s,π×π',ψ)
proved the local Langlands conjectures for the general linear group GLn(K) for positive characteristic local fields K. gave an exposition of their work.
proved the local Langlands conjectures for the general linear group GLn(K) for characteristic 0 local fields K. gave another proof. and gave expositions of their work.
Local Langlands conjectures for other groups
and discuss the Langlands conjectures for more general groups. As of 2011, the Langlands conjectures for arbitrary reductive groups G are not as precise as the ones for general linear groups, and it is unclear what the correct way of stating them should be. Roughly speaking, admissible representations of a reductive group are grouped into disjoint finite sets called L-packets, which should correspond to some classes of homomorphisms, called L-parameters, from the Weil–Deligne group to the L-group of G.proved the Langlands conjectures for groups over the archimedean local fields R and C by giving the Langlands classification
Langlands classification
In mathematics, the Langlands classification is a classification of irreducible representations of a reductive Lie group G, suggested by Robert Langlands...
of their irreducible admissible representations (up to infinitesimal equivalence), or, equivalently, of their irreducible
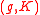 -modules
-modules(g,K)-module
In mathematics, more specifically in the representation theory of reductive Lie groups, a -module is an algebraic object, first introduced by Harish-Chandra, used to deal with continuous infinite-dimensional representations using algebraic techniques...
.
proved the local Langlands conjectures for the symplectic similitude group GSp(4) and used that in to deduce it for the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(4).
External links
- The work of Robert Langlands
- Automorphic Forms - The local Langlands conjecture Lecture by Richard Taylor

