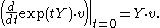(g,K)-module
Encyclopedia
In mathematics
, more specifically in the representation theory of reductive Lie groups, a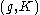
-module is an algebraic object, first introduced by Harish-Chandra
, used to deal with continuous infinite-dimensional representations using algebraic techniques. Harish-Chandra showed that the study of irreducible unitary representations
of a real reductive Lie group, G, could be reduced to the study of irreducible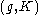
-modules, where 
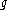is the Lie algebra
of G and K is a maximal compact subgroup
of G.
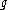be its Lie algebra, and K a maximal compact subgroup with Lie algebra 
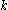. A 
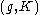-module is defined as follows: it is a vector space
V that is both a Lie algebra representation of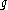
and a group representation
of K (without regard to the topology
of K) satisfying the following three conditions
In the above, the dot,
, denotes both the action of 
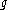on V and that of K. The notation Ad(k) denotes the adjoint action of G on 
, and Kv is the set of vectors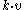 
as k varies over all of K.
The first condition can be understood as follows: if G is the general linear group
GL(n, R), then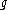
is the algebra of all n by n matrices, and the adjoint action of k on X is kXk−1; condition 1 can then be read as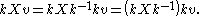
In other words, it is a compatibility requirement among the actions of K on V,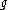
on V, and K on 
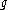. The third condition is also a compatibility condition, this time between the action of 
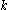on V viewed as a sub-Lie algebra of 
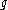and its action viewed as the differential of the action of K on V.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in the representation theory of reductive Lie groups, a
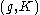-module is an algebraic object, first introduced by Harish-ChandraHarish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, used to deal with continuous infinite-dimensional representations using algebraic techniques. Harish-Chandra showed that the study of irreducible unitary representations
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of a real reductive Lie group, G, could be reduced to the study of irreducible
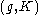-modules, where 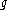is the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G and K is a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of G.
Definition
Let G be a real Lie group. Let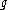 be its Lie algebra, and K a maximal compact subgroup with Lie algebr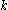a . A 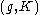-module is defined as follows: it is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V that is both a Lie algebra representation of
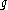and a group representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of K (without regard to the topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
of K) satisfying the following three conditions
- 1. for any v ∈ V, k ∈ K, and X ∈
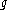
- 2. for any v ∈ V, Kv spans a finite-dimensional subspace of V on which the action of K is continuous
- 3. for any v ∈ V and Y ∈
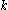
In the above, the dot,
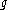, denotes both the action of on V and that of K. The notation Ad(k) denotes the adjoint action of G on , and Kv is the set of vectors 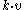as k varies over all of K.The first condition can be understood as follows: if G is the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n, R), then
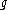is the algebra of all n by n matrices, and the adjoint action of k on X is kXk−1; condition 1 can then be read as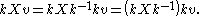In other words, it is a compatibility requirement among the actions of K on V,
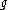on V, and K on 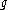. The third condition is also a compatibility condition, this time between the action of 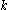on V viewed as a sub-Lie algebra of 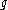and its action viewed as the differential of the action of K on V.