Local flatness
Encyclopedia
In topology
, a branch of mathematics
, local flatness is a property of a submanifold in a topological manifold
of larger dimension
.
Suppose a d dimensional manifold N is embedded in an n dimensional manifold M (where d < n). If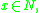
we say N is locally flat at x if there is a neighborhood 
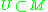of x such that 
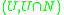is homeomorphic to the pair 
.
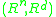However, if M has boundary
that contains N, we make a special definition: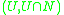
should be homeomorphic to 
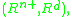where 
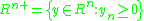and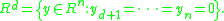 
(The first definition assumes that, if M has any boundary, x is not a boundary point of M.)
We call N locally flat in M if every point of N is locally flat.
Local flatness of an embedding implies strong properties not shared by all embeddings. Brown (1962) proved that if d = n − 1, then N is collared; that is, it has a neighborhood which is homeomorphic to N × [0,1] with N itself corresponding to N × 1/2 (if N is in the interior of M) or N × 0 (if N is in the boundary of M).
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, local flatness is a property of a submanifold in a topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
of larger dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
.
Suppose a d dimensional manifold N is embedded in an n dimensional manifold M (where d < n). If
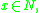we say N is locally flat at x if there is a neighborhood 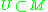of x such that 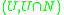is homeomorphic to the pair 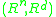.However, if M has boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
that contains N, we make a special definition:
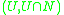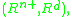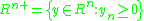should be homeomorphic to where and 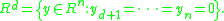(The first definition assumes that, if M has any boundary, x is not a boundary point of M.)
We call N locally flat in M if every point of N is locally flat.
Local flatness of an embedding implies strong properties not shared by all embeddings. Brown (1962) proved that if d = n − 1, then N is collared; that is, it has a neighborhood which is homeomorphic to N × [0,1] with N itself corresponding to N × 1/2 (if N is in the interior of M) or N × 0 (if N is in the boundary of M).