The London equations, developed by brothers Fritz

Fritz London

Fritz Wolfgang London was a German theoretical physicist. His fundamental contributions to the theories of chemical bonding and of intermolecular forces are today considered classic and are discussed in standard textbooks of physical chemistry.With his brother Heinz, he made a significant...

 and Heinz London

Heinz London

Heinz London was a German Physicist. He worked with his brother Fritz on superconductivity, discovering the London equations when working in Oxford, at the Clarendon Laboratory; these equations gave a first explanation to the Meissner effect...

 in 1935,
relate current to electromagnetic fields in and around a superconductor. Arguably the simplest meaningful description of superconducting phenomena, they form the genesis of almost any modern introductory text on the subject.
A major triumph of the equations is their ability to explain the Meissner effect

Meissner effect

The Meissner effect is the expulsion of a magnetic field from a superconductor during its transition to the superconducting state. The German physicists Walther Meissner and Robert Ochsenfeld discovered the phenomenon in 1933 by measuring the magnetic field distribution outside superconducting tin...

,
wherein a material exponentially expels all internal magnetic fields as it crosses the superconducting threshold.

Formulations

There are two London equations when expressed in terms of measurable fields:
Here 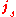is the superconducting current, E and B are respectively the electric and magnetic fields within the superconductor,

is the charge of an electron & proton,

is electron mass, and

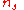
is a phenomenological constant loosely associated with a number density of superconducting carriers.
Throughout this article Gaussian (cgs) units

Gaussian units

Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...

 are employed.

On the other hand, if one is willing to abstract away slightly, both the expressions above can more neatly be written in terms of a single "London Equation"

in terms of the vector potential

Vector potential

In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....

 A:

The last equation suffers from only the disadvantage that it is not gauge invariant, but is true only in the London gauge, where the divergence of A is zero.

London Penetration Depth

If the second of London's equations is manipulated by applying Ampere's law

Ampère's law

In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...

,,
then the result is the differential equation
Thus, the London equations imply a characteristic length scale, 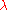, over which external magnetic fields are exponentially suppressed. This value is the London penetration depth

London penetration depth

In superconductors, the London penetration depth characterizes the distance to which a magnetic field penetrates into a superconductor and becomes equal to 1/e times that of the magnetic field at the surface of the superconductor...

.

A simple example geometry is a flat boundary between a superconductor within free space where the magnetic field outside the superconductor is a constant value pointed parallel to the superconducting boundary plane in the z direction. If x leads perpendicular to the boundary then the solution inside the superconductor may be shown to be


From here the physical meaning of the London penetration depth can perhaps most easily be discerned.

Original arguments

While it is important to note that the above equations cannot be derived in any conventional sense of the word,
the Londons did follow a certain intuitive logic in the formulation of their theory. Substances across a stunningly wide range of composition behave roughly according to Ohm's law, which states that current is proportional to electric field. However, such a linear relationship is impossible in a superconductor for, almost by definition, the electrons in a superconductor flow with no resistance whatsoever. To this end, the brothers London imagined electrons as if they were free electrons under the influence of a uniform external electric field. According to the Lorentz force law
these electrons should encounter a uniform force, and thus they should in fact accelerate uniformly. This is precisely what the first London equation states.

To obtain the second equation, take the curl of the first London equation and apply Faraday's law

Faraday's law

Faraday's law may refer to the following:*Faraday's laws of electrolysis in chemistry*Faraday's law of induction, also known as Faraday-Lenz Law, in electromagnetism physics**The Maxwell–Faraday equation...

,,
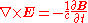to obtain

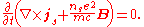
As it currently stands, this equation permits both constant and exponentially decaying solutions. The Londons recognized from the Meissner effect that constant nonzero solutions were nonphysical, and thus postulated that not only was the time derivative of the above expression equal to zero, but also that the expression in the parentheses must be identically zero. This results in the second London equation.

Canonical momentum arguments

It is also possible to justify the London equations by other means.

Current density is defined according to the equation
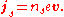
Taking this expression from a classical description to a quantum mechanical one, we must replace values j and v by the expectation values of their operators. The velocity operator
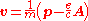
is defined by dividing the gauge-invariant, kinematic momentum operator by the particle mass m.

We may then make this replacement in the equation above. However, an important assumption from the microscopic theory of superconductivity

BCS theory

BCS theory — proposed by Bardeen, Cooper, and Schrieffer in 1957 — is the first microscopic theory of superconductivity since its discovery in 1911. The theory describes superconductivity as a microscopic effect caused by a "condensation" of pairs of electrons into a boson-like state...

is that the superconducting state of a system is the ground state, and according to a theorem of Bloch's,
in such a state the canonical momentum p is zero. This leaves
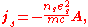
which is the London equation according to the second formulation above.