Long code (mathematics)
Encyclopedia
In theoretical computer science
and coding theory
, the long code is an error-correcting code
that is locally decodable. Long codes have an extremely poor rate, but play a fundamental role in the theory of hardness of approximation
.
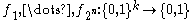for 
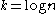be the list of all functions from 
.
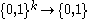Then the long code encoding of a message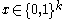
is the string 
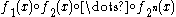where 
denotes concatenation of strings.
This string has length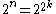
.
The Walsh-Hadamard code is a subcode of the long code, and can be obtained by only using functions
that are linear function
s when interpreted as functions
on the finite field
with two elements. Since there are only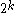
such functions, the block length of the Walsh-Hadamard code is 
.
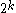An equivalent definition of the long code is as follows:
The Long code encoding of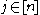
is defined to be the truth table of the Boolean dictatorship function on the 
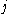th coordinate, i.e., the truth table of 
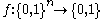with 
.
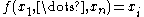Thus, the Long code encodes a
-bit string as a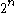 
-bit string.
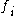computing the 
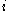th bit of the output is different from any function 
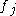computing the 
th bit of the output for 
.
Among all codes that do not contain repetitions, the long code has the longest possible output.
Moreover, it contains all non-repeating codes as a subcode.
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
and coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, the long code is an error-correcting code
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
that is locally decodable. Long codes have an extremely poor rate, but play a fundamental role in the theory of hardness of approximation
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
.
Definition
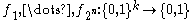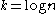Let for be the list of all functions from 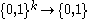.Then the long code encoding of a message
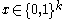is the string 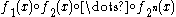where denotes concatenation of strings.This string has length
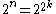.The Walsh-Hadamard code is a subcode of the long code, and can be obtained by only using functions
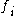that are linear functionLinear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
s when interpreted as functions
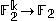on the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with two elements. Since there are only
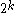such functions, the block length of the Walsh-Hadamard code is 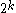.An equivalent definition of the long code is as follows:
The Long code encoding of
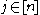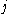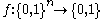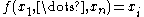is defined to be the truth table of the Boolean dictatorship function on the th coordinate, i.e., the truth table of with .Thus, the Long code encodes a
-bit string as a 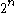-bit string.Properties
The long code does not contain repetitions, in the sense that the function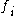 computing the 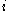th bit of the output is different from any function 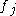computing the th bit of the output for .Among all codes that do not contain repetitions, the long code has the longest possible output.
Moreover, it contains all non-repeating codes as a subcode.