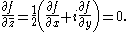Looman–Menchoff theorem
Encyclopedia
In the mathematical
field of complex analysis
, the Looman–Menchoff theorem states that a continuous
complex
-valued function defined in an open set
of the complex plane
is holomorphic if and only if it satisfies the Cauchy–Riemann equations. It is thus a generalization of a theorem by Goursat, which instead of assuming the continuity of f, assumes its Fréchet differentiability
when regarded as a function from a subset of R2 to R2.
A complete statement of the theorem is as follows:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the Looman–Menchoff theorem states that a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued function defined in an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is holomorphic if and only if it satisfies the Cauchy–Riemann equations. It is thus a generalization of a theorem by Goursat, which instead of assuming the continuity of f, assumes its Fréchet differentiability
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
when regarded as a function from a subset of R2 to R2.
A complete statement of the theorem is as follows:
- Let Ω be an open set in C and f : Ω → C a continuous function. Suppose that the partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s
and 
exist everywhere but a countable set in Ω. Then f is holomorphic if and only if it satisfies the Cauchy–Riemann equation:
