
Lorentz space
Encyclopedia
In mathematical analysis
, Lorentz spaces, introduced by George Lorentz in the 1950s, are generalisations of the more familiar Lp spaces
.
The Lorentz spaces are denoted by Lp,q. Like the Lp spaces, they are characterized by a norm
(technically a quasinorm) that encodes information about the "size" of a function, just as the Lp norm does. The two basic qualitative notions of "size" of a function are: how tall is graph of the function, and how spread out is it. The Lorentz norms provide tighter control over both qualities than the Lp norms, by exponentially rescaling the measure in both the range (the p) and the domain (the q). The Lorentz norms, like the Lp norms, are invariant under arbitrary rearrangements of the values of a function.
s ƒ on X such that the following quasinorm is finite
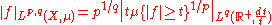
where 0 < p < ∞ and 0 < q ≤ ∞. Thus, when q < ∞,
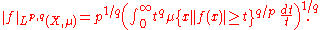
and when q = ∞,
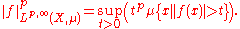
It is also conventional to set L∞,∞(X,μ) = L∞(X,μ).
ƒ defined on a measure space, (X, μ), its decreasing rearrangement function,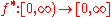 can be defined as
can be defined as
where dƒ is the so-called distribution function of ƒ, given by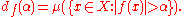
Here, for notational convenience,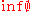 is defined to be ∞.
is defined to be ∞.
Given these definitions, for p, q ∈ (0, ∞), the Lorentz norms are given by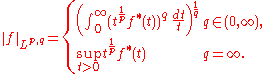
. Further, Lp,∞ coincides with weak Lp. They are quasi-Banach spaces (that is quasi-normed spaces which are also complete) and are normable for p ∈ (1, ∞), q ∈ [1, ∞]. Lp,q is a subspace of Lp,r whenever q < r.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Lorentz spaces, introduced by George Lorentz in the 1950s, are generalisations of the more familiar Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
The Lorentz spaces are denoted by Lp,q. Like the Lp spaces, they are characterized by a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
(technically a quasinorm) that encodes information about the "size" of a function, just as the Lp norm does. The two basic qualitative notions of "size" of a function are: how tall is graph of the function, and how spread out is it. The Lorentz norms provide tighter control over both qualities than the Lp norms, by exponentially rescaling the measure in both the range (the p) and the domain (the q). The Lorentz norms, like the Lp norms, are invariant under arbitrary rearrangements of the values of a function.
Definition
The Lorentz space on a measure space (X,μ) is the space of complex-valued measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s ƒ on X such that the following quasinorm is finite
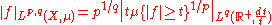
where 0 < p < ∞ and 0 < q ≤ ∞. Thus, when q < ∞,
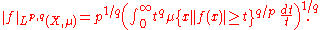
and when q = ∞,
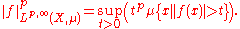
It is also conventional to set L∞,∞(X,μ) = L∞(X,μ).
Decreasing rearrangements
The quasinorm is invariant under rearranging the values of the function ƒ, essentially by definition. In particular, given a complex-valued measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
ƒ defined on a measure space, (X, μ), its decreasing rearrangement function,
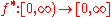 can be defined as
can be defined as
where dƒ is the so-called distribution function of ƒ, given by
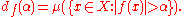
Here, for notational convenience,
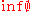 is defined to be ∞.
is defined to be ∞.Given these definitions, for p, q ∈ (0, ∞), the Lorentz norms are given by
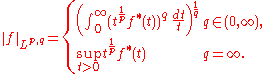
Properties
The Lorentz spaces are genuinely generalisations of the Lp spaces in the sense that for any p, Lp,p = Lp, which follows from Cavalieri's principleCavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
. Further, Lp,∞ coincides with weak Lp. They are quasi-Banach spaces (that is quasi-normed spaces which are also complete) and are normable for p ∈ (1, ∞), q ∈ [1, ∞]. Lp,q is a subspace of Lp,r whenever q < r.

